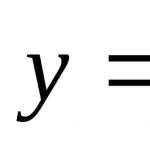Иркутский государственный университет путей сообщения
Лабораторная работа № 16
по дисциплине«Сопротивление материалов»
ОПЫТНОЕ ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ СИЛ
ПРИ ПРОДОЛЬНОМ ИЗГИБЕ
Кафедра ПМ
Лабораторная работа № 16
Опытное определение критических сил при продольном изгибе
Цель работы: исследование явления потери устойчивости сжатого стального стержня в упругой
стадии. Экспериментальное определение значений критических нагрузок сжатых
стержней при различных способах закрепления и сравнение их с теоретическими
значениями.
Общие положения
Сжатые стержни недостаточно проверять на прочность по известному условию:
 ,
,
где [σ] – допускаемое напряжение для материала стержня, P – сжимающая сила, F – площадь поперечного сечения.
В практической деятельности инженеры имеют дело с подвергающимися сжатию гибкими стержнями, тонкими сжатыми пластинами, тонкостенными конструкциями, выход из строя которых вызывается ен потерей несущей способности, а потерей устойчивости.
Под потерей устойчивости понимается потеря первоначальной формы равновесия.
В сопротивлении материалов рассматривается устойчивость элементов конструкций, работающих на сжатие.
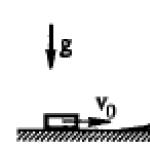
Рассмотрим длинный тонкий стержень (рис. 1), нагруженный осевой сжимающей силой P .
P < P кр P > P кр

Рис. 1. Стержень, нагруженный осевой сжимающей силой P .
При малых значениях силы F стержень сжимается, оставаясь прямолинейным. Причем, если стержень отклонить от этого положения небольшой поперечной нагрузкой, то он изогнется, но при снятии ее стержень возвращается в прямолинейное состояние. Это значит, что при данной силе P прямолинейная форма равновесия стержня устойчива.
Если продолжить увеличивать сжимающую силу P , то при некотором ее значении прямолинейная форма равновесия становится неустойчивой и возникает новая форма равновесия стержня - криволинейная (рис. 1, б). Вследствие изгиба стержня в его сечениях появится изгибающий момент, который вызовет дополнительные напряжения, и стержень может внезапно разрушиться.
Искривление длинного стержня, сжимаемого продольной силой, называется продольным изгибом .
Наибольшее значение сжимающей силы, при котором прямолинейная форма равновесия стержня устойчива, называется критическим - P кр .
При достижении критической нагрузки происходит резкое качественное изменение первоначальной формы равновесия, что ведет к выходу конструкции из строя. Поэтому критическая сила рассматривается как разрушающая нагрузка.
Формулы Эйлера и Ясинского
Задачу определения критической силы сжатого стержня впервые решил член Петербургской академии наук Л. Эйлер в 1744 г. Формула Эйлера имеет вид
 (1)
(1)
где Е – модуль упругости материала стержня; J min - наименьший момент инерции поперечного сечения стержня (поскольку искривление стержня при потере устойчивости происходит в плоскости наименьшей жесткости, т. е. поперечные сечения стержня поворачиваются вокруг оси, относительно которой момент инерции минимален, т.е. либо вокруг оси x , либо вокруг оси y );
(μ·l ) – приведенная длина стержня, это произведение длины стержня l на коэффициент μ, зависящий от способов закрепления концов стержня.
Коэффициент μ называют коэффициентом приведения длины ;его значение для наиболее часто встречающихся случаев закрепления концов стержня приведены на рис. 2:
а - оба конца стержня закреплены шарнирно и могут сближаться;
б - один конец жестко защемлен, другой свободен;
в - один конец закреплен шарнирно, второй имеет «поперечно-плавающую заделку»;
г - один конец жестко защемлен, второй имеет «поперечно-плавающую заделку»;
д - один конец заделан жестко, на другом шарнирно-подвижная опора;
е - оба конца жестко защемлены, но могут сближаться.
Из этих примеров видно, что коэффициент μ представляет собой величину, обратную числу полуволн упругой линии стержня при потере устойчивости.

Рис. 2. Коэффициент μ для наиболее часто
встречающихся случаев закрепления концов стержня.
Нормальное напряжение в поперечном сечении сжатого стержня, соответствующее критическому значению сжимающей силы, также называется критическим.
Определим его исходя из формулы Эйлера:
 (2)
(2)
Геометрическую характеристику сечения i min , определяемую по формуле
называют радиусом инерции сечения (относительно оси с J min ). Для прямоугольного сечения

С учетом (3) формула (2) примет вид:
 (4)
(4)
Отношение приведенной длины стержня к минимальному радиусу инерции его поперечного сечения по предложению профессора Санкт-Петербургского института инженеров путей сообщения Ф.С. Ясинского (1856-1899) называют гибкостью стержня и обозначают буквой λ :
В этой безразмерной величине одновременно отражаются такие параметры: длина стержня, способ его закрепления и характеристика поперечного сечения.
Окончательно, подставив (5) в формулу (4), получим
При выводе формулы Эйлера предполагалось, что материал стержня упруг и следует закону Гука. Следовательно, формулу Эйлера можно применять только при напряжениях, меньших предела пропорциональности σ пц , т. е. когда

Этим условием определяется предел применимости формулы Эйлера:
Величину, стоящую в правой части этого неравенства, называют предельной гибкостью :

ее значение зависит от физико-механических свойств материала стержня.
Для низкоуглеродистой стали Ст. 3, у которой σ пц = 200 МПа, Е = 2· 10 5 МПа:
Аналогично можно вычислить значение предельной гибкости для других материалов: для чугуна λ пред = 80, для сосны λ пред = 110.
Таким образом, формула Эйлера применима для стержней, гибкость которых больше или равна предельной гибкости , т. е.
λ ≥ λ пред
Понимать это надо так: если гибкость стержня больше предельной гибкости, то критическую силу надо определять по формуле Эйлера.
При λ < λ пред формула Эйлера для стержней неприменима. В этих случаях, когда гибкость стержней меньше предельной, при расчетах пользуются эмпирической формулой Ясинского :
σ кр = a – b·λ , (7)
где а и b - определяемые опытным путем коэффициенты, постоянные для данного материала; они имеют размерность напряжения.
При некотором значении гибкости λ о напряжение σ кр , вычисленное по формуле (7), становится равным предельному напряжению при сжатии, т. е. пределу текучести σ т для пластичных материалов или пределу прочности при сжатии σ вс – для хрупких материалов. Стержни малой гибкости (λ < λ о )рассчитывают не на устойчивость, а на прочность при простом сжатии.
Таким образом, в зависимости от гибкости расчет сжатых стержней на устойчивость производится различно.
Задача определения критической силы была впервые поставлена и решена математиком Л.Эйлером*, в дальнейшем она была обобщена на другие случаи концевых закреплений стержня.
Эта формула имеет вид:
где Е – модуль упругости первого рода материала стержня;
I min – минимальный главный центральный момент инерции поперечного сечения стержня;
l – длина стержня;
m - коэффициент приведения длины стержня, зависящий от способа закрепления его концов;
m l – приведенная длина стержня.
На рис. 8.2 показаны наиболее распространенные способы закрепления концов сжатого стержня (штриховыми линиями изображены примерные формы упругих линий стержней при нагрузках, больших критических):
1) оба конца стержня закреплены шарнирно - m = 1 (рис. 8.2,а);
2) один конец жестко защемлен, а другой свободен - m = 2 (рис. 8.2,б);
3) оба конца жестко защемлены, но могут сближаться - m = 0,5 (рис. 8.2,в); 4) один конец стержня закреплен жестко, а другой – шарнирно - m = 0,7 (рис. 8.2,г).
| m = 0,7 |
| m = 0,5 |
| m = 2 |
| m = 1 |
| F |
| F |
| F |
| а) |
| б) |
| в) |
| г) |
| Рис. 8.2 |
| F |
Формула Эйлера справедлива лишь при условии, что потеря устойчивости происходит в пределах упругих деформаций стержня, т.е. в пределах действия закона Гука.
Если обе части формулы Эйлера (8.3) разделить на площадь поперечного сечения стержня А, то получим так называемое критическое напряжение s кр , т.е. то напряжение, которое возникает в сечении стержня под действием критической силы F kp . При этом критическое напряжение не должно превышать предела пропорциональности:
где i min – минимальный радиус инерции.
Момент инерции берется минимальный потому, что стержень стремится изогнуться в плоскости наименьшей жесткости.
Разделим числитель и знаменатель формулы (8.4) на минимальный момент инерции I min , представленный формулой (8.5):
где - безразмерная величина называемая гибкостью стержня.
Условие применимости формулы Эйлера удобно выразить через гибкость стержня. Выразим из неравенства (8.6) значение l:
Правую часть этого неравенства обозначают l пред и называют предельной гибкостью стержня из данного материала, т.е.
Таким образом, получим окончательное условие применимости формулы Эйлера - l ³ l пред. Формула Эйлера применима, когда гибкость стержня не меньше предельной гибкости .
Так, например, для стали Ст.3 (Е = 2*10 5 Мпа; s пц = 200 МПа):
т.е. формула Эйлера применима в этом случае при l ³ 100.
Аналогично можно вычислить предельную гибкость и для других материалов.
В конструкциях нередко встречаются стержни, у которых l < l пред. Расчет таких стержней ведется по эмпирической формуле, выведенной профессором Ф.С.Ясинским* на основании обширного опытного материала:
где a, b, c – коэффициенты, зависящие от свойств материала.
В таблице приведены значения а, b и c для некоторых материалов, а также значения гибкостей, в пределах которых применима формула (8.9).
Таблица 8.1
При гибкости l < l 0 стержни можно рассчитывать на прочность без учета опасности потери устойчивости.
Из формул Эйлера и Ясинского следует, что значение критической силы возрастает с увеличением минимального момента инерции поперечного сечения стержня. Так как устойчивость стержня определяется значением минимального момента инерции его поперечного сечения, то, очевидно, рациональны сечения, у которых главные моменты инерции равны между собой. Стойка, имеющая такое сечение, обладает равноустойчивостью во всех направлениях. Из сечений такого типа следует выбирать такие, которые обладают наибольшим моментом инерции при наименьшей площади (затрате материала). Таким сечением является кольцевое сечение.
На рис. 8.3 представлена диаграмма зависимости критического напряжения в стержне от его гибкости. В зависимости от гибкости стержни условно делят на три категории. Стержни большой гибкости (l ³ l пред)
рассчитывают на устойчивость по формуле Эйлера; стержни средней гибкости (l 0 £l £l пред)
рассчитывают на устойчивость по формуле Ясинского; стержни малой гибкости (l
ДЕТАЛИ МАШИН
«Соединения деталей машин»
В процессе изготовления машины некоторые ее детали соединяют между собой, при этом образуются неразъемные или разъемные соединения.
Неразъемными называют соединения, которые невозможно разобрать без разрушения или повреждения деталей. К ним относятся заклепочные, сварные и клеевые соединения.
Разъемными называют соединения, которые можно разбирать и вновь собирать без повреждения деталей. К разъемным соединениям относятся резьбовые, шпоночные, зубчатые (шлицевые) и другие.
Задача определения критической силы для сжатого стержня впервые была решена в 1744 году выдающимся математиком Леонардом Эйлером. Формула для критической силы была выведена Эйлером на примере идеального прямого стержня постоянного сечения, шарнирно закрепленного на концах (Рис.2).
Одна из опор стержня допускает возможность продольного перемещения соответствующего конца стержня. Собственный вес стержня не учитывалась. Искомая формула выглядела:
![]() (2)
(2)
Формула Эйлера (2) для критической силы выводилась для стержня с шарнирным закрепления концов. Этот случай закрепления концов стержня принято называть основным случаем. В этом случае на длине стержня укладывается одна полуволна синусоиды. Однако, в практике встречаются различные другие случаи закрепления концов стержня. На рис.3 приведены некоторые из них, которые наиболее часто встречаются.

Для определения значения критической силы для каждого из приведенных случаев закрепления концов на практике применяется способ, который использует геометрическую аналогию между поведением упругой линии сжатого стержня с шарнирным закреплением концов (основной случай) и другим способом закрепления концов стержня. Согласно этим способом все остальные случаев закрепления концов стержня сводится к основному путем введения так называемой сводной или свободной длины стержня.
Сводной или свободной длиной стержня называется условная длина шарнирно закрепленного стержня, имеет такую же критическую силу, как и стержень с заданным закреплением концов. Судить о сводную длину стержня можно по числу полуволн, которые укладываются на длине стержня. С геометрической аналогии следует, что в пределах сводной длины стержень с произвольным закреплением концов вести себя так же, как стержень с шарнирным закреплением концов.
Сводная длина стержня вычисляется следующим образом: , где длина стержня с заданным закреплением концов; коэффициент сводной длины.
Из определения сводной длины следует, что коэффициент есть такое число, на которое необходимо умножить длину стержня с заданным закреплением концов, чтобы получить такую длину условного стержня с шарнирным закреплением концов, на котором заключается одна полуволна синусоиды.
Для стержня, изображенного на рис.3 , а длина условного стержня с шарнирным закреплением концов должно быть в два раза больше, чем заданная длина стержня. Верхняя часть условного стержня с шарнирным закреплением концов вести себя точно так же, как и стержень с заданным закреплением концов. Коэффициент возведения длины для этого случая равна. На рис.3 , в одна полуволна размещается на длине, составляющей 0,7 реальной длины стержня. Коэффициент возведения длины в этом случае составляет. Для случая жесткого закрепления обоих концов стержня (Рис.3 , г) длина полуволны, замеренная между двумя точками перегиба, составляет половину длины стержня. Для этого случая коэффициент. Для основного случая (Рис.3 , б) коэффициент, поскольку на его длине укладывается одна полуволна и, следовательно, сведена длина стержня равна реальной его длине.
Преобразуем формулу Эйлера (2) , подставляя в нее вместо реальной длины стержня сводную длину. Получаем формулу Эйлера для критической силы в окончательном виде:
 (3)
(3)
На рис.3 приведены значения критической силы для стержней с различными условиями закрепления концов при одинаковых начальной длине и жесткости поперечного сечения. Следует отметить, что наибольшее значение критическая сила достигает для стержня с жестким закреплением концов (Рис.3 , г). В этом случае критическая сила оказывается в четыре раза больше, чем для основного случае закрепления концов. Наименее эффективным типом закрепления концов стержня является случай, приведенный на рис.3 , а. Критическая сила в этом случае оказывается в четыре раза меньше, чем для основного случая.
6.Структурный анализ плоского механизма. Формула Чебышева
Механизмом называется механическая система тел, в которой заданныедвижения одного или нескольких тел преобразуются в необходимое движениедругих тел. Таким образом, механизмы служат для преобразованиядвижения.
Механизмы часто являются составной частью машины (см. определение ма-шины в ) преобразуя движение ее двигателя
в необходимое движение рабочего органа.
Рассмотрим структуру механизма на примере
кривошипно-ползунного механизма (рис.1).
Механизм состоит из звеньев 1, 2, 3 и 4
которые представляют одну деталь или груп-
пу жестко соединенных деталей, имеющих
общий закон движения.
Звено 1 – ведущее звено, закон движе-
ния которого задан. Это звено также называют
входным звеном. Оно всегда обозначается со
стрелкой.
Звенья 2, 3 – ведомые звенья; звено 3 – называют также исполнительным
или выходным звеном. Оно совершает движение для получения, которого по-
лучен механизм.
Звено 4 – стойка или базовое звено, на котором устанавливаются осталь-
ные звенья. Движение всех звеньев в механизме рассматривается относительно
стойки.
Определим критическую силу для центрально сжатого стержня, шарнирно опертого по концам (рис. 13.4). При небольших значениях силы Р ось стержня остается прямой и в его сечениях возникают напряжения центрального сжатия о = P/F. При критическом значении силы Р = Р становится воз- можной искривленная форма равновесия стержня.
Возникает продольный изгиб. Изгибающий момент в произвольном сечении х стержня равен
Важно заметить, что изгибающий момент определяется для деформированного состояния стержня.
Если предположить, что напряжения изгиба, возникающие в поперечных сечениях стержня от действия критической силы, не превосходят предел пропорциональности материала о пц и прогибы стержня малы, то можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня (см. § 9.2)
Введя обозначение
получим вместо (13.2) следующее уравнение:
Общее решение этого уравнения имеет вид
Это решение содержит три неизвестных: постоянные интегрирования Cj, С 2 и параметр к, так как величина критической силы также неизвестна. Для определения этих трех величин имеются только два граничных условия: и(0) = 0, v(l ) = 0. Из первого граничного условия следует, что С 2 = 0, а из второго получим
Из этого равенства следует, что либо С { = 0, либо sin kl = 0. В случае С, = 0 прогибы во всех сечениях стержня равны нулю, что противоречит исходному предположению задачи. Во втором случае kl = пк, где п - произвольное целое число. С учетом этого по формулам (13.3) и (13.5) получим

Рассмотренная задача является задачей на собственные значения. Найденные числа к = пк/1 называются собственными числами, а соответствующие им функции - собственными функциями.
Как видно из (13.7), в зависимости от числа п сжимающая сила Р (я) , при которой стержень находится в изогнутом состоянии, теоретически может принимать целый ряд значений. При этом согласно (13.8) стержень изгибается по п полуволнам синусоиды (рис. 13.5).
Наименьшее значение силы будет при п = 1:
Эта сила носит название первой критической силы. При этом kl = к и изогнутая ось стержня представляет собой одну полуволну синусоиды (рис. 13.5, а):
где С{ 1} =/ - прогиб в середине длины стержня, что следует из (13.8) при п = 1 их = 1/2.
Формула (13.9) была получена Леонардом Эйлером и называется формулой Эйлера для критической силы.
Все формы равновесия (рис. 13.5), кроме первой (п = 1), неустойчивы и потому не представляют практического интереса. Формы равновесия, соответствующие п - 2, 3, ..., будут устойчивыми, если в точках перегиба упругой линии (точки С и С" на рис. 13.5, б, в) ввести дополнительные шарнирные опоры.

Полученное решение обладает двумя особенностями. Во-первых, решение (13.10) не является единственным, так как произвольная постоянная Cj (1) =/ осталась неопределенной, несмотря на использование всех граничных условий. В результате прогибы оказались определены с точностью до постоянного множителя. Во- вторых, это решение не дает возможности описать состояние стержня при Р > Р кр. Из (13.6) следует, что при Р = Р кр стержень может иметь искривленную форму равновесия при условии kl = к. Если же Р > Р кр, то kl Ф п, и тогда должно быть Cj (1) = 0. Это означает, что v = 0, то есть стержень после искривления при Р = Р кр вновь приобретает прямолинейную форму при Р > Р. Очевидно, что это противоречит физическим представлениям об изгибе стержня.
Эти особенности связаны с тем, что выражение (13.1) для изгибающего момента и дифференциальное уравнение (13.2) получены для деформированного состояния стержня, в то время как при постановке граничного условия на конце х = / осевое перемещение и в этого конца (рис. 13.6) вследствие изгиба не учитывалось. Действительно, если пренебречь укорочением стержня за счет центрального сжатия, то нетрудно представить, что прогибы стержня будут иметь вполне определенные значения, если задать величину и в.
Из этого рассуждения становится очевидным, что для определения зависимости прогибов от величины сжимающей силы Р необходимо вместо граничного условия v(l) = 0 использовать уточненное граничное условие v(l - и в) = 0. При этом установлено, что если сила превосходит критическое значение всего на 1+2%, прогибы становятся достаточно большими и необходимо пользоваться точным нелинейным дифференциальным уравнением продольного изгиба
Это уравнение отличается от приближенного уравнения (13.4) первым слагаемым, представляющим собой точное выражение для кривизны изогнутой оси стержня (см. § 9.2).
Решение уравнения (13.11) достаточно сложно и выражается через полный эллиптический интеграл первого рода.