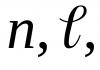Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l 1 = 18,84 см, l 2 = 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см - это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Очевидно, что границей любого круга является окружность. Поэтому понятие периметра круга совпадает с таким понятием, как длина окружности . Поэтому вначале вспомним, что является окружностью, и какие понятия с ней связаны.
Понятие окружности
Определение 1
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Определение 2
Центром окружности будем называть точку, которая задается в рамках определения 1.
Определение 3
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки (Рис. 1).
В декартовой системе координат $xOy$ мы также можем ввести уравнение любой окружности. Обозначим центр окружности точкой $X$, которая будет иметь координаты $(x_0,y_0)$. Пусть радиус этой окружности равняется $τ$. Возьмем произвольную точку $Y$, координаты которой обозначим через $(x,y)$ (рис. 2).
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
$|XY|=\sqrt{(x-x_0)^2+(y-y_0)^2}$
С другой стороны, $|XY|$ - это расстояние от любой точки окружности до выбранного нами центра. То есть, по определению 3, получим, что $|XY|=τ$, следовательно
$\sqrt{(x-x_0)^2+(y-y_0)^2}=τ$
$(x-x_0)^2+(y-y_0)^2=τ^2$ (1)
Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.
Длина окружности (периметр круга)
Будем выводить длину произвольной окружности $C$ с помощью её радиуса, равного $τ$.
Будем рассматривать две произвольные окружности. Обозначим их длины через $C$ и $C"$, у которых радиусы равняются $τ$ и $τ"$. Будем вписывать в эти окружности правильные $n$-угольники, периметры которых равняются $ρ$ и $ρ"$, длины сторон которых равняются $α$ и $α"$, соответственно. Как мы знаем, сторона вписанного в окружность правильного $n$ – угольника равняется
$α=2τsin\frac{180^0}{n}$
Тогда, будем получать, что
$ρ=nα=2nτ\frac{sin180^0}{n}$
$ρ"=nα"=2nτ"\frac{sin180^0}{n}$
$\frac{ρ}{ρ"}=\frac{2nτsin\frac{180^0}{n}}{2nτ"\frac{sin180^0}{n}}=\frac{2τ}{2τ"}$
Получаем, что отношение $\frac{ρ}{ρ"}=\frac{2τ}{2τ"}$ будет верным независимо от значения числа сторон вписанных правильных многоугольников . То есть
$\lim_{n\to\infty}(\frac{ρ}{ρ"})=\frac{2τ}{2τ"}$
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть $n→∞$), будем получать равенство:
$lim_{n\to\infty}(\frac{ρ}{ρ"})=\frac{C}{C"}$
Из последних двух равенств получим, что
$\frac{C}{C"}=\frac{2τ}{2τ"}$
$\frac{C}{2τ}=\frac{C"}{2τ"}$
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
$\frac{C}{2τ}=const$
Эту постоянную принять называть числом «пи» и обозначать $π$. Приближенно, это число будет равняться $3,14$ (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
$\frac{C}{2τ}=π$
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
Пример задач
Пример 1
Найти периметр круга, который вписан в квадрат со стороной, равной $α$.
Пусть нам дан квадрат $ABCD$, в который вписана окружность с центром $O$. Изобразим рисунок по условию задачи (рис. 3).
Очевидно, что центр окружности будет совпадать с центром квадрата, в которой она вписана. Так как квадрат описан вокруг окружности, то его стороны будут касательными к ней, то есть радиус, проведенный, к примеру, к стороне $AB$ будет перпендикулярен к ней. Значит, диаметр окружности равняется стороне квадрата. То есть
$τ=\frac{α}{2}$
По формуле периметра круга, получим, что
$C=2π\cdot \frac{α}{2}=πα$
Ответ: $πα$.
Пример 2
Найти периметр круга, который описан у прямоугольного треугольника с катетами, равными $α$ и $β$.
Пусть нам дан треугольник $ABC$ с прямым углом $C$, у которой описана окружность с центром $O$. Как мы знаем, диаметром такой окружности является гипотенуза такого треугольника. То есть $|AO|=|OB|=|OC|=τ$ (рис. 4).
По теореме Пифагора, гипотенуза равняется
$|AB|=\sqrt{α^2+β^2}$
$|AO|=τ=\frac{\sqrt{α^2+β^2}}{2}$
Периметр круга, по формуле, равняется
$C=2π\cdot \frac{\sqrt{α^2+β^2}}{2}=π\sqrt{α^2+β^2}$
Ответ: $π\sqrt{α^2+β^2}$.
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Вконтакте
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две - А и В - можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры - это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр - расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С - это искомая величина, D - диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере - длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С - длина, r - радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек - это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве - рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
