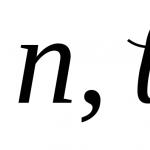Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.
Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:
Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.
Пример 1. Найти предел .
Решение. Подстановка вместо x нуля приводит к неопределённости:
![]() .
.
В знаменателе - синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:
![]() .
.
В знаменателе - синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе. Для чего? Чтобы представить 3x = a и получить выражение .
И приходим к разновидности первого замечательного предела:
потому что неважно, какая буква (переменная) в этой формуле стоит вместо икса.
Умножаем икс на три и тут же делим:
 .
.
В соответствии с замеченным первым замечательным пределом производим замену дробного выражения:
Теперь можем окончательно решить данный предел:
 .
.
Пример 2. Найти предел .
Решение. Непосредственная подстановка вновь приводит к неопределённости "нуль делить на нуль":
![]() .
.
Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:
 .
.
Пример 3. Найти предел .
Решение. При подстановке вновь получаем неопределённость "нуль делить на нуль":
 .
.
Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:
 .
.
Пример 4. Найти предел .
Решение. Вновь получаем неопределённость "нуль делить на нуль":
![]() .
.
Можем получить отношение двух первых замечательных пределов. Делим и числитель, и знаменатель на икс. Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс умножаем на 3 и тут же делим на 3. Получаем:

Пример 5. Найти предел .
Решение. И вновь неопределённость "нуль делить на нуль":
Помним из тригонометрии, что тангенс - это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:
 .
.
Пример 6. Найти предел .
Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела. Представляем его как отношение синуса к косинусу.
Обычно второй замечательный предел записывают в такой форме:
\begin{equation} \lim_{x\to\infty}\left(1+\frac{1}{x}\right)^x=e\end{equation}
Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $e\approx{2{,}718281828459045}$. Если сделать замену $t=\frac{1}{x}$, то формулу (1) можно переписать в следующем виде:
\begin{equation} \lim_{t\to{0}}\biggl(1+t\biggr)^{\frac{1}{t}}=e\end{equation}
Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное - выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $\frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^\infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+\infty$ или $-\infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела . Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Пример №1
Вычислить предел $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right)^{4x+7}$.
Сразу отметим, что основание степени (т.е. $\frac{3x+1}{3x-5}$) стремится к единице:
$$ \lim_{x\to\infty}\frac{3x+1}{3x-5}=\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{3+\frac{1}{x}}{3-\frac{5}{x}} =\frac{3+0}{3-0} =1. $$
При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $\lim_{x\to\infty}(4x+7)=\infty$.
Основание степени стремится к единице, показатель степени - к бесконечности, т.е. мы имеем дело с неопределенностью $1^\infty$. Применим формулу для раскрытия этой неопределённости. В основании степени формулы расположено выражение $1+\frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $\frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $\frac{3x+1}{3x-5}$ под вид $1+\frac{1}{x}$. Для начала прибавим и вычтем единицу:
$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right)^{4x+7} =|1^\infty| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} $$
Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
$$ \frac{3x+1}{3x-5}-1 =\frac{3x+1}{3x-5}-\frac{3x-5}{3x-5} =\frac{3x+1-3x+5}{3x-5} =\frac{6}{3x-5}. $$
Так как $\frac{3x+1}{3x-5}-1=\frac{6}{3x-5}$, то:
$$ \lim_{x\to\infty}\left(1+ \frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{4x+7} $$
Продолжим «подгонку». В выражении $1+\frac{1}{x}$ формулы в числителе дроби находится 1, а в нашем выражении $1+\frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
$$ 1+\frac{6}{3x-5} =1+\frac{1}{\frac{3x-5}{6}} $$
Таким образом,
$$ \lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{4x+7} $$
Итак, основание степени, т.е. $1+\frac{1}{\frac{3x-5}{6}}$, подогнано под вид $1+\frac{1}{x}$, который требуется в формуле . Теперь начнём работать с показателем степени. Заметьте, что в формуле выражения, стоящие в показатели степени и в знаменателе, одинаковы:
Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $\frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $\frac{6}{3x-5}$. Итак, имеем:
$$ \lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =\lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{\frac{3x-5}{6}}\right)^{\frac{6\cdot(4x+7)}{3x-5}} $$
Отдельно рассмотрим предел дроби $\frac{6\cdot(4x+7)}{3x-5}$, расположенной в степени:
$$ \lim_{x\to\infty}\frac{6\cdot(4x+7)}{3x-5} =\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{6\cdot\left(4+\frac{7}{x}\right)}{3-\frac{5}{x}} =6\cdot\frac{4}{3} =8. $$
Ответ : $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}=e^{-\frac{2}{9}}$.
Пример №4
Найти предел $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)$.
Так как при $x>0$ имеем $\ln(x+1)-\ln{x}=\ln\left(\frac{x+1}{x}\right)$, то:
$$ \lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right) =\lim_{x\to+\infty}\left(x\cdot\ln\left(\frac{x+1}{x}\right)\right) $$
Раскладывая дробь $\frac{x+1}{x}$ на сумму дробей $\frac{x+1}{x}=1+\frac{1}{x}$ получим:
$$ \lim_{x\to+\infty}\left(x\cdot\ln\left(\frac{x+1}{x}\right)\right) =\lim_{x\to+\infty}\left(x\cdot\ln\left(1+\frac{1}{x}\right)\right) =\lim_{x\to+\infty}\left(\ln\left(\frac{x+1}{x}\right)^x\right) =\ln{e} =1. $$
Ответ : $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)=1$.
Пример №5
Найти предел $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}$.
Так как $\lim_{x\to{2}}(3x-5)=6-5=1$ и $\lim_{x\to{2}}\frac{2x}{x^2-4}=\infty$, то мы имеем дело с неопределенностью вида $1^\infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:
$$ \lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}} =\left|\begin{aligned}&t=x-2;\;x=t+2\\&t\to{0}\end{aligned}\right| =\lim_{t\to{0}}\biggl(1+3t\biggr)^{\frac{2t+4}{t^2+4t}}=\\ =\lim_{t\to{0}}\biggl(1+3t\biggr)^{\frac{1}{3t}\cdot 3t\cdot\frac{2t+4}{t^2+4t}} =\lim_{t\to{0}}\left(\biggl(1+3t\biggr)^{\frac{1}{3t}}\right)^{\frac{6\cdot(t+2)}{t+4}} =e^3. $$
Можно решить данный пример и по-иному, используя замену: $t=\frac{1}{x-2}$. Разумеется, ответ будет тем же:
$$ \lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}} =\left|\begin{aligned}&t=\frac{1}{x-2};\;x=\frac{2t+1}{t}\\&t\to\infty\end{aligned}\right| =\lim_{t\to\infty}\left(1+\frac{3}{t}\right)^{t\cdot\frac{4t+2}{4t+1}}=\\ =\lim_{t\to\infty}\left(1+\frac{1}{\frac{t}{3}}\right)^{\frac{t}{3}\cdot\frac{3}{t}\cdot\frac{t\cdot(4t+2)}{4t+1}} =\lim_{t\to\infty}\left(\left(1+\frac{1}{\frac{t}{3}}\right)^{\frac{t}{3}}\right)^{\frac{6\cdot(2t+1)}{4t+1}} =e^3. $$
Ответ : $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}=e^3$.
Пример №6
Найти предел $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} $.
Выясним, к чему стремится выражение $\frac{2x^2+3}{2x^2-4}$ при условии $x\to\infty$:
$$ \lim_{x\to\infty}\frac{2x^2+3}{2x^2-4} =\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{2+\frac{3}{x^2}}{2-\frac{4}{x^2}} =\frac{2+0}{2-0}=1. $$
Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела:
$$ \lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} =|1^\infty| =\lim_{x\to\infty}\left(1+\frac{2x^2+3}{2x^2-4}-1\right)^{3x}=\\ =\lim_{x\to\infty}\left(1+\frac{7}{2x^2-4}\right)^{3x} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{3x}=\\ =\lim_{x\to\infty}\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{\frac{2x^2-4}{7}\cdot\frac{7}{2x^2-4}\cdot 3x} =\lim_{x\to\infty}\left(\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{\frac{2x^2-4}{7}}\right)^{\frac{21x}{2x^2-4}} =e^0 =1. $$
Ответ : $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x}=1$.
|
Первый замечательный предел. Вывод первого замечательного предела представляет интерес с точки зрения приложения теории пределов, и поэтому мы предлагаем Вам его практически целиком. Рассмотрим поведение функции
|
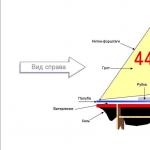
Тогда явно площадь DМОА < площадь сектора МОА < площадьDСОА (см. рис. 1).
S D МОА
=

S МОА = =
= S D C ОА =
S D C ОА =
Вернувшись к упомянутому неравенству и удвоив его, получим:
sin x < x < tg x .
После почленного деления наsinx
:
 или
или

Поскольку
 ,
то переменная
,
то переменная заключена между двумя величинами,
имеющими один и тот же предел, т.е. , на
основании теоремы о пределе промежуточной
функции предыдущего пункта имеем:
заключена между двумя величинами,
имеющими один и тот же предел, т.е. , на
основании теоремы о пределе промежуточной
функции предыдущего пункта имеем:
-первый замечательный предел .
Пример. Вычислите пределы функций, используя первый замечательный предел:





Ответ.
1) 1, 2) 0, 3)

Задание: Вычислите предел функции, используя первый замечательный предел:

Ответ:-2.
Второй замечательный предел.
Для вывода второго замечательного предела введем определение числа е :
Определение.
Предел переменной
величины
 при
при называется числом
е
:
называется числом
е
:
- Второй замечательный предел
Число е – иррациональное число. Его значение с десятью верными знаками после запятой обычно округляют до одного верного знака после запятой:
e = 2,7182818284…»2,7.
Теорема. Функция
 при
х
, стремящемся к бесконечности,
стремится к пределу
е
:
при
х
, стремящемся к бесконечности,
стремится к пределу
е
:

Пример. Вычислите пределы функций:

Решение.
Согласно свойствам пределов, предел степени равен степени предела, т. е.:


Кроме того, аналогичным образом можно
доказать, что



Ответ. 1)е 3 , 2) е 2 , 3)е 4 .
Задание. Вычислите предел функции, используя второй замечательный предел:

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
О твет:
е -5
твет:
е -5
Непрерывность функции Непрерывность функции в точке
Определение. Функция f ( x ), x Î ( a ; b ) x о Î ( a ; b ), если предел функции f ( x ) в точке х о существует и равен значению функции в этой точке:
 .
.
Согласно данному определению, непрерывность функции f (x ) в точкех о означает выполнимость следующих условий:
функция f (x ) должна быть определена в точкех о ;
у функции f (x ) должен существовать предел в точкех о ;
предел функции f (x ) в точкех о должен совпадать со значением функции в этой точке.
Пример.
Функция f
(x
)
=
x
2
определена на всей числовой прямой и
непрерывна в точкех
= 1 посколькуf
(1)
= 1 и

Непрерывность функции на множестве
Определение. Функция f(x), называется непрерывной на интервале (a; b), если она непрерывна в каждой точке этого интервала.
Если функция непрерывна в некоторой точке, то эта точка называется точкой непрерывности данной функции. В тех случаях, когда предел функции в данной точке не существует или его значение не совпадает со значением функции в данной точке, то функция называется разрывной в этой точке, а сама точка – точкой разрыва функции f(x).
Свойства непрерывных функций.
1) Сумма конечного числа функций, непрерывных в точке а,
2) Произведение конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке.
3) Отношение конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точкеа.
Пример.
Функция f (x ) = x п , гдеn Î N , непрерывна на всей числовой прямой. Доказать этот факт можно, используя свойство 2 и непрерывность функцииf (x ) = x .
Функция f (x ) = с x п (с – константа) непрерывна на всей числовой прямой, исходя из свойства 2 и примера 1.
Теорема 1. Многочлен есть функция, непрерывная на всей числовой прямой.
Теорема 2 . Любая дробно-рациональная функция непрерывна в каждой точке своей области определения .
Пример.

Определение
Функция
f
(
x
)
называется непрерывной в точке
х
= а
, если в этой точке ее приращение
 стремится
к нулю, когда приращение аргумента
стремится
к нулю, когда приращение аргумента стремится
к нулю, или иначе: функция
f
(х)
называется непрерывной в точке
х = а
, если в этой точке
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции, т. е. если
стремится
к нулю, или иначе: функция
f
(х)
называется непрерывной в точке
х = а
, если в этой точке
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции, т. е. если

Собраны формулы, свойства и теоремы, применяемые при решении задач, допускающих решение с помощью первого замечательного предела. Даны подробные решения примеров с использованием первого замечательного предела его следствий.
СодержаниеСм. также: Доказательство первого замечательного предела и его следствий
Применяемые формулы, свойства и теоремы
Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется первый замечательный предел и его следствия.
Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.
- Первый замечательный предел и его следствия:
. - Тригонометрические формулы для синуса, косинуса , тангенса и котангенса :
;
;
;
при , ;
;
;
;
;
;
.
Примеры решений
Пример 1
Для этого.
1. Вычисляем предел .
Поскольку функция непрерывна для всех x
,
и в том числе в точке ,
то
.
2. Поскольку функция не определена (и, следовательно, не является непрерывной) при ,
то нам нужно убедиться, что существует такая проколотая окрестность точки ,
на которой .
В нашем случае при .
Поэтому это условие выполнено.
3. Вычисляем предел .
В нашем случае он равен первому замечательному пределу:
.
Таким образом,
.
Аналогичным образом, находим предел функции в знаменателе:
;
при ;
.
И наконец, применяем арифметические свойства предела функции :
.
Применим .
При .
Из таблицы эквивалентных функций находим:
при ;
при .
Тогда .
Пример 2
Найдите предел:
.
Решение с помощью первого замечательного предела
При , , . Это неопределенность вида 0/0 .
Преобразуем функцию за знаком предела:
.
Сделаем замену переменной .
Поскольку и при ,
то
.
Аналогичным образом имеем:
.
Поскольку функция косинус непрерывна на всей числовой оси, то
.
Применяем арифметические свойства пределов:
.
Решение с помощью эквивалентных функций
Применим теорему о замене функций эквивалентными в пределе частного .
При .
Из таблицы эквивалентных функций находим:
при ;
при .
Тогда .
Пример 3
Найти предел:
.
Подставим в числитель и знаменатель дроби:
;
.
Это неопределенность вида 0/0
.
Попробуем решить этот пример с помощью первого замечательного предела. Поскольку в нем значение переменной стремится к нулю, то сделаем подстановку, чтобы новая переменная стремилась не к , а к нулю. Для этого от x перейдем к новой переменной t , сделав подстановку , . Тогда при , .
Предварительно преобразуем функцию за знаком предела, умножив числитель и знаменатель дроби на :
.
Подставим и воспользуемся приведенными выше тригонометрическими формулами.
;
;
.
Функция непрерывна при .
Находим ее предел:
.
Преобразуем вторую дробь и применим первый замечательный предел:
.
В числителе дроби мы сделали подстановку .
Применяем свойство предела произведения функций:
.
Пример 4
Найти предел:
.
При , , . У нас неопределенность вида 0/0 .
Преобразуем функцию под знаком предела. Применим формулу:
.
Подставим :
.
Преобразуем знаменатель:
.
Тогда
.
Поскольку и при ,
то сделаем подстановку ,
и применим теорему о пределе сложной функции и первый замечательный предел:
.
Применяем арифметические свойства предела функции:
.
Пример 5
Найдите предел функции:
.
Нетрудно убедиться, что в этом примере мы имеем неопределенность вида 0/0
.
Для ее раскрытия, применим результат предыдущей задачи, согласно которому
.
Введем обозначение:
(П5.1)
.
Тогда
(П5.2)
.
Из (П5.1) имеем:
.
Подставим в исходную функцию:
,
где ,
,
;
;
;
.
Используем (П5.2) и непрерывность функции косинус. Применяем арифметические свойства предела функции.
,
здесь m
- отличное от нуля число, ;
;
;
.
Пример 6
Найти предел:
.
При ,
числитель и знаменатель дроби стремятся к 0
.
Это неопределенность вида 0/0
.
Для ее раскрытия, преобразуем числитель дроби:
.
Применим формулу:
.
Подставим :
;
,
где .
Применим формулу:
.
Подставим :
;
,
где .
Числитель дроби:
.
Функция за знаком предела примет вид:
.
Найдем предел последнего множителя, учитывая его непрерывность при :
.
Применим тригонометрическую формулу:
.
Подставим ,
.
Тогда
.
Разделим числитель и знаменатель на ,
применим первый замечательный предел и одно из его следствий:
.
Окончательно имеем:
.
Примечание 1.
Также можно было применить формулу
.
Тогда .
Первый замечательный предел часто применяется для вычисления пределов содержащих синус, арксинус, тангенс, арктангенс и получающихся при них неопределенностей ноль делить на ноль.
Формула
Формула первого замечательного предела имеет вид: $$ \lim_{\alpha\to 0} \frac{\sin\alpha}{\alpha} = 1 $$
Замечаем, что при $ \alpha\to 0 $ получается $ \sin\alpha \to 0 $, тем самым в числетеле и в знаменателе имеем нули. Таким образом формула первого замечательного предела нужна для раскрытия неопределенностей $ \frac{0}{0} $.
Для применения формулы необходимо, чтобы были соблюдены два условия:
- Выражения, содержащиеся в синусе и знаменателе дроби совпадают
- Выражения, стоящие в синусе и знаменателе дроби стремятся к нулю
Внимание! $ \lim_{x\to 0} \frac{\sin(2x^2+1)}{2x^2+1} \neq 1 $ Хотя выражения под синусом и в знаменателе одинаковые, однако $ 2x^2+1 = 1 $, при $ x\to 0 $. Не выполнено второе условие, поэтому применять формулу НЕЛЬЗЯ!
Следствия
Достаточно редко в задания можно увидеть чистый первый замечательный предел, в котором можно сразу было бы записать ответ. На практике всё немного сложнее выглядит, но для таких случаев будет полезно знать следствия первого замечательного предела. Благодаря им можно быстро вычислить нужные пределы.
$$ \lim_{\alpha\to 0} \frac{\alpha}{\sin\alpha} = 1 $$
$$ \lim_{\alpha\to 0} \frac{\sin(a\alpha)}{\sin(b\alpha)} = \frac{a}{b} $$
$$ \lim_{\alpha\to 0} \frac{tg\alpha}{\alpha} = 1 $$
$$ \lim_{\alpha\to 0} \frac{\arcsin\alpha}{\alpha} = 1 $$
$$ \lim_{\alpha\to 0} \frac{arctg\alpha}{\alpha} = 1 $$
Примеры решений
Рассмотрим первый замечательный предел, примеры решения которого на вычисление пределов содержащих тригонометрические функции и неопределенность $ \bigg[\frac{0}{0}\bigg] $
| Пример 1 |
| Вычислить $ \lim_{x\to 0} \frac{\sin2x}{4x} $ |
| Решение |
|
Рассмотрим предел и заметим, что в нём присутствует синус. Далее подставим $ x = 0 $ в числитель и знаменатель и получим неопределенность нуль делить на нуль: $$ \lim_{x\to 0} \frac{\sin2x}{4x} = \frac{0}{0} $$ Уже два признака того, что нужно применять замечательный предел, но есть небольшой нюанс: сразу применить формулу мы не сможем, так как выражение под знаком синуса отличается от выражения стоящего в знаменателе. А нам нужно, чтобы они были равны. Поэтому с помощью элементарных преобразований числителя мы превратим его в $ 2x $. Для этого мы вынесем двойку из знаменателя дроби отдельным множителем. Выглядит это так: $$ \lim_{x\to 0} \frac{\sin2x}{4x} = \lim_{x\to 0} \frac{\sin2x}{2\cdot 2x} = $$ $$ = \frac{1}{2} \lim_{x\to 0} \frac{\sin2x}{2x} = \frac{1}{2}\cdot 1 = \frac{1}{2} $$ Обратите внимание, что в конце $ \lim_{x\to 0} \frac{\sin2x}{2x} = 1 $ получилось по формуле. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ \lim_{x\to 0} \frac{\sin2x}{4x} =\frac{1}{2} $$ |
| Пример 2 |
| Найти $ \lim_{x\to 0} \frac{\sin(x^3+2x)}{2x-x^4} $ |
| Решение |
|
Как всегда сначала нужно узнать тип неопределенности. Если она нуль делить на нуль, то обращаем внимание на наличие синуса: $$ \lim_{x\to 0} \frac{\sin(x^3+2x)}{2x-x^4} = \frac{0}{0} = $$ Данная неопределенность позволяет воспользоваться формулой первого замечательного предела, но выражение из знаменателя не равно аргументу синуса? Поэтом "в лоб" применить формулу нельзя. Необходимо умножить и разделить дробь на аргумент синуса: $$ = \lim_{x\to 0} \frac{(x^3+2x)\sin(x^3+2x)}{(2x-x^4)(x^3+2x)} = $$ Теперь по свойствам пределов расписываем: $$ = \lim_{x\to 0} \frac{(x^3+2x)}{2x-x^4}\cdot \lim_{x\to 0} \frac{\sin(x^3+2x)}{(x^3+2x)} = $$ Второй предел как раз подходит под формулу и равен единице: $$ = \lim_{x\to 0} \frac{x^3+2x}{2x-x^4}\cdot 1 = \lim_{x\to 0} \frac{x^3+2x}{2x-x^4} = $$ Снова подставляем $ x = 0 $ в дробь и получаем неопределенность $ \frac{0}{0} $. Для её устранения достоточно вынести за скобки $ x $ и сократить на него: $$ = \lim_{x\to 0} \frac{x(x^2+2)}{x(2-x^3)} = \lim_{x\to 0} \frac{x^2+2}{2-x^3} = $$ $$ = \frac{0^2 + 2}{2 - 0^3} = \frac{2}{2} = 1 $$ |
| Ответ |
| $$ \lim_{x\to 0} \frac{\sin(x^3+2x)}{2x-x^4} = 1 $$ |
| Пример 4 |
| Вычислить $ \lim_{x\to0} \frac{\sin2x}{tg3x} $ |
| Решение |
|
Вычисление начнём с подстановки $ x=0 $. В результате получаем неопределенность $ \frac{0}{0} $. Предел содержит синус и тангенс, что намекает на возможное развитие ситуации с использованием формулы первого замечательного предела. Преобразуем числитель и знаменатель дроби под формулу и следствие: $$ \lim_{x\to0} \frac{\sin2x}{tg3x} = \frac{0}{0} = \lim_{x\to0} \frac{\frac{\sin2x}{2x}\cdot 2x}{\frac{tg3x}{3x}\cdot 3x} = $$ Теперь видим в числителе и знаменателе появились выражения подходящие под формулу и следствия. Аргумент синуса и аргумент тангенса совпадают для соответствующих знаменателей $$ = \lim_{x\to0} \frac{1\cdot 2x}{1\cdot 3x} = \frac{2}{3} $$ |
| Ответ |
| $$ \lim_{x\to0} \frac{\sin2x}{tg2x} = \frac{2}{3} $$ |
В статье: "Первый замечательный предел, примеры решения" было рассказано о случаях, в которых целесообразно использовать данную формулу и её следствия.
 при
при .
Для этого рассмотрим окружность
радиуса 1; обозначим центральный угол
МОВ черезх
, при этом
.
Для этого рассмотрим окружность
радиуса 1; обозначим центральный угол
МОВ черезх
, при этом .
.