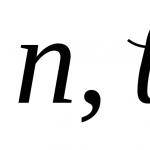Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx :
Вроде бы все понятно. Но попробуйте посчитать по этой формуле, скажем, производную функции f (x ) = x 2 + (2x + 3) · e x · sin x . Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.
Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.
Производные элементарных функций
Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.
Итак, производные элементарных функций:
| Название | Функция | Производная |
| Константа | f (x ) = C , C ∈ R | 0 (да-да, ноль!) |
| Степень с рациональным показателем | f (x ) = x n | n · x n − 1 |
| Синус | f (x ) = sin x | cos x |
| Косинус | f (x ) = cos x | − sin x (минус синус) |
| Тангенс | f (x ) = tg x | 1/cos 2 x |
| Котангенс | f (x ) = ctg x | − 1/sin 2 x |
| Натуральный логарифм | f (x ) = ln x | 1/x |
| Произвольный логарифм | f (x ) = log a x | 1/(x · ln a ) |
| Показательная функция | f (x ) = e x | e x (ничего не изменилось) |
Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:
(C · f )’ = C · f ’.
В общем, константы можно выносить за знак производной. Например:
(2x 3)’ = 2 · (x 3)’ = 2 · 3x 2 = 6x 2 .
Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.
Производная суммы и разности
Пусть даны функции f (x ) и g (x ), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:
- (f + g )’ = f ’ + g ’
- (f − g )’ = f ’ − g ’
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h )’ = f ’ + g ’ + h ’.
Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g , и тогда останется лишь одна формула — производная суммы.
f (x ) = x 2 + sin x; g (x ) = x 4 + 2x 2 − 3.
Функция f (x ) — это сумма двух элементарных функций, поэтому:
f ’(x ) = (x 2 + sin x )’ = (x 2)’ + (sin x )’ = 2x + cos x;
Аналогично рассуждаем для функции g (x ). Только там уже три слагаемых (с точки зрения алгебры):
g ’(x ) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · (x 2 + 1).
Ответ:
f
’(x
) = 2x
+ cos x;
g
’(x
) = 4x
· (x
2 + 1).
Производная произведения
Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike ">равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:
(f · g ) ’ = f ’ · g + f · g ’
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
Задача. Найти производные функций: f (x ) = x 3 · cos x; g (x ) = (x 2 + 7x − 7) · e x .
Функция f (x ) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x ) = (x 3 · cos x )’ = (x 3)’ · cos x + x 3 · (cos x )’ = 3x 2 · cos x + x 3 · (− sin x ) = x 2 · (3cos x − x · sin x )
У функции g (x ) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g (x ) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x ) = ((x 2 + 7x − 7) · e x )’ = (x 2 + 7x − 7)’ · e x + (x 2 + 7x − 7) · (e x )’ = (2x + 7) · e x + (x 2 + 7x − 7) · e x = e x · (2x + 7 + x 2 + 7x −7) = (x 2 + 9x ) · e x = x (x + 9) · e x .
Ответ:
f
’(x
) = x
2 · (3cos x
− x
· sin x
);
g
’(x
) = x
(x
+ 9) · e
x
.
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.
Если есть две функции f (x ) и g (x ), причем g (x ) ≠ 0 на интересующем нас множестве, можно определить новую функцию h (x ) = f (x )/g (x ). Для такой функции тоже можно найти производную:
Неслабо, да? Откуда взялся минус? Почему g 2 ? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.
Задача. Найти производные функций:
В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:
По традиции, разложим числитель на множители — это значительно упростит ответ:
Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f (x ) = sin x и заменить переменную x , скажем, на x 2 + ln x . Получится f (x ) = sin (x 2 + ln x ) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.
Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:
f ’(x ) = f ’(t ) · t ’, если x заменяется на t (x ).
Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.
Задача. Найти производные функций: f (x ) = e 2x + 3 ; g (x ) = sin (x 2 + ln x )
Заметим, что если в функции f (x ) вместо выражения 2x + 3 будет просто x , то получится элементарная функция f (x ) = e x . Поэтому делаем замену: пусть 2x + 3 = t , f (x ) = f (t ) = e t . Ищем производную сложной функции по формуле:
f ’(x ) = f ’(t ) · t ’ = (e t )’ · t ’ = e t · t ’
А теперь — внимание! Выполняем обратную замену: t = 2x + 3. Получим:
f ’(x ) = e t · t ’ = e 2x + 3 · (2x + 3)’ = e 2x + 3 · 2 = 2 · e 2x + 3
Теперь разберемся с функцией g (x ). Очевидно, надо заменить x 2 + ln x = t . Имеем:
g ’(x ) = g ’(t ) · t ’ = (sin t )’ · t ’ = cos t · t ’
Обратная замена: t = x 2 + ln x . Тогда:
g ’(x ) = cos (x 2 + ln x ) · (x 2 + ln x )’ = cos (x 2 + ln x ) · (2x + 1/x ).
Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.
Ответ:
f
’(x
) = 2 · e
2x
+ 3 ;
g
’(x
) = (2x
+ 1/x
) · cos (x
2 + ln x
).
Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.
Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:
(x n )’ = n · x n − 1
Немногие знают, что в роли n вполне может выступать дробное число. Например, корень — это x 0,5 . А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.
Задача. Найти производную функции:
Для начала перепишем корень в виде степени с рациональным показателем:
f (x ) = (x 2 + 8x − 7) 0,5 .
Теперь делаем замену: пусть x 2 + 8x − 7 = t . Находим производную по формуле:
f ’(x ) = f ’(t ) · t ’ = (t 0,5)’ · t ’ = 0,5 · t −0,5 · t ’.
Делаем обратную замену: t = x 2 + 8x − 7. Имеем:
f ’(x ) = 0,5 · (x 2 + 8x − 7) −0,5 · (x 2 + 8x − 7)’ = 0,5 · (2x + 8) · (x 2 + 8x − 7) −0,5 .
Наконец, возвращаемся к корням:
Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.
Как найти?
Чтобы найти производную функции нужно знать таблицу производных элементарных функций и применять основные правила дифференцирования :
- Вынос константы за знак производной: $$ (Cu)" = C(u)" $$
- Производная суммы /разности функций: $$ (u \pm v)" = (u)" \pm (v)" $$
- Производная произведения двух функций: $$ (u \cdot v)" = u"v + uv" $$
- Производная дроби : $$ \bigg (\frac{u}{v} \bigg)" = \frac{u"v - uv"}{v^2} $$
- Производная сложной функции : $$ (f(g(x)))" = f"(g(x)) \cdot g"(x) $$
Примеры решения
| Пример 1 |
| Найти производную функции $ y = x^3 - 2x^2 + 7x - 1 $ |
| Решение |
|
Производная суммы/разности функций равна сумме/разности производных: $$ y" = (x^3 - 2x^2 + 7x - 1)" = (x^3)" - (2x^2)" + (7x)" - (1)" = $$ Используя правило производной степенной функции $ (x^p)" = px^{p-1} $ имеем: $$ y" = 3x^{3-1} - 2 \cdot 2 x^{2-1} + 7 - 0 = 3x^2 - 4x + 7 $$ Так же было учтено, что производная от константы равна нулю. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y" = 3x^2 - 4x + 7 $$ |
С
правочные материалы по теме «производная». Базовый школьный уровень.
Теоретические сведения для учеников, преподавателей и репетиторов по математике. В помощь к проведению занятий.
Определение: производной функции в точке называется предел отношения приращения функции к приращению переменной, то есть
Таблица производных основных математических функций:

Правила вычисления производных
Производная суммы двух любых выражений равна сумме производных этих выражений (производная суммы равна сумме производных)
Производная разности двух любых выражений равна разности производных этих слагаемых (производная разности равна разности производных).
Производная от произведения
двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго (сумма поочередно взятых производных от множителей).
Комментарий репетитора по математике:
когда я короткими фразами напоминаю ученику о правиле вычисления производной от произведения, я говорю так: производная первого множителя на второй плюс обмен штрихами!
![]()
Производная от частного
двух выражений равна частному разности поочередно взятых производных от множителей и квадрата знаменателя.
Производная от произведения числа на функцию . Чтобы найти производную от произведения числа на буквенное выражение (на функцию) нужно умножить это число на производную этого буквенного выражения.
Производная сложной функции:
Для вычисления производной сложной функции необходимо найти производную внешней функции и умножить ее на производную внутренней функции.
Ваши комментарии и отзывы к странице с производными:
Александр С.
Очень нужна была таблица. В интернете одна из самых. За пояснения и правила тоже огромное спасибо. Хотя бы по одному примеру ещё к ним и вообще было бы отлично было. Еще раз огромное спасибо.
Колпаков А.Н, репетитор по математике: хорошо, постараюсь в ближайшее время дополнить страницу примерами.
Виртуальный математический справочник.
Колпаков Александр Николаевич, репетитор по математике.
Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.
Для их обозначения будем использовать латинские буквы f, g и др.
Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g" означает, что мы будем находить производную функции g.
Таблица производных
Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
- (sin x)"=cos x
- (cos x)"= –sin x
- (x n)"=n x n-1
- (e x)"=e x
- (ln x)"=1/x
- (a x)"=a x ln a
- (log a x)"=1/x ln a
- (tg x)"=1/cos 2 x
- (ctg x)"= – 1/sin 2 x
- (arcsin x)"= 1/√(1-x 2)
- (arccos x)"= - 1/√(1-x 2)
- (arctg x)"= 1/(1+x 2)
- (arcctg x)"= - 1/(1+x 2)
Пример 1. Найдите производную функции y=500.
Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).
Пример 2. Найдите производную функции y=x 100 .
Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).
(x 100)"=100 x 99
Пример 3. Найдите производную функции y=5 x
Это показательная функция, вычислим ее производную по формуле 4.
Пример 4. Найдите производную функции y= log 4 x
Производную логарифма найдем по формуле 7.
(log 4 x)"=1/x ln 4
Правила дифференцирования
Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С - константа.
1. Постоянный коэффициент можно выносить за знак производной
Пример 5. Найдите производную функции y= 6*x 8
Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.
(6*x 8)" = 6*(x 8)"=6*8*x 7 =48* x 7
2. Производная суммы равна сумме производных
(f + g)"=f" + g"
Пример 6. Найдите производную функции y= x 100 +sin x
Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)"=100 x 99 и (sin x)"=cos x. Производная суммы будет равна сумме данных производных:
(x 100 +sin x)"= 100 x 99 +cos x
3. Производная разности равна разности производных
(f – g)"=f" – g"
Пример 7. Найдите производную функции y= x 100 – cos x
Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)"= – sin x.
(x 100 – cos x)"= 100 x 99 + sin x
Пример 8. Найдите производную функции y=e x +tg x– x 2 .
В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:
(e x)"=e x , (tg x)"=1/cos 2 x, (x 2)"=2 x. Тогда производная исходной функции равна:
(e x +tg x– x 2)"= e x +1/cos 2 x –2 x
4. Производная произведения
(f * g)"=f" * g + f * g"
Пример 9. Найдите производную функции y= cos x *e x
Для этого сначала найдем производного каждого множителя (cos x)"=–sin x и (e x)"=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.
(cos x* e x)"= e x cos x – e x *sin x
5. Производная частного
(f / g)"= f" * g – f * g"/ g 2
Пример 10. Найдите производную функции y= x 50 /sin x
Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)"=50 x 49 и (sin x)"= cos x. Подставив в формулу производной частного получим:
(x 50 /sin x)"= 50x 49 *sin x – x 50 *cos x/sin 2 x
Производная сложной функции
Сложная функция - это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:
(u (v))"=u"(v)*v"
Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) - сложная функция. Функцию u назовем внешней, а v - внутренней.
Например:
y=sin (x 3) - сложная функция.
Тогда y=sin(t) - внешняя функция
t=x 3 - внутренняя.
Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.
(sin t)"=cos (t) - производная внешней функции (где t=x 3)
(x 3)"=3x 2 - производная внутренней функции
Тогда (sin (x 3))"= cos (x 3)* 3x 2 - производная сложной функции.