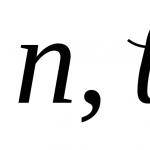Броуновское движение частиц в жидкости. Броуновское движение. Что такое броуновское движение

План:

1 Сущность явления
2 Открытие броуновского движения
- 2.1 Наблюдение
3 Теория броуновского движения
- 3.1 Построение классической теории
- 3.2 Экспериментальное подтверждение
- 3.3 Броуновское движение как немарковский случайный процесс

Введение

Тепловое движение частиц вещества, таких как атомы и молекулы - причина броуновского движения

Бро́уновское движе́ние - в естествознании, беспорядочное движение микроскопических, видимых, взвешенных в жидкости (или газе) частиц (броуновские частицы) твёрдого вещества (пылинки, крупинки взвеси, частички пыльцы растения и так далее), вызываемое тепловым движением частиц жидкости (или газа). Не следует смешивать понятия «броуновское движение» и «тепловое движение»: броуновское движение является следствием и свидетельством существования теплового движения.

В математике, а точнее в теории случайных процессов, броуновское движение (или винеровский процесс ) - это гауссовский процесс с независимыми приращениями, у которого математическое ожидание равно нулю, а среднеквадратическое отклонение равно .

1. Сущность явления

Броуновское движение происходит из-за того, что все жидкости и газы состоят из атомов или молекул - мельчайших частиц, которые находятся в постоянном хаотическом тепловом движении, и потому непрерывно толкают броуновскую частицу с разных сторон. Было установлено, что крупные частицы с размерами более 5 мкм в броуновском движении практически не участвуют (они неподвижны или седиментируют),более мелкие частицы (менее 3мкм) двигаются поступательно по весьма сложным траекториям или вращаются. Когда в среду погружено крупное тело, то толчки, происходящие в огромном количестве, усредняются и формируют постоянное давление. Если крупное тело окружено средой со всех сторон, то давление практически уравновешивается, остаётся только подъёмная сила Архимеда - такое тело плавно всплывает или тонет. Если же тело мелкое, как броуновская частица, то становятся заметны флуктуации давления, которые создают заметную случайно изменяющуюся силу, приводящую к колебаниям частицы. Броуновские частицы обычно не тонут и не всплывают, а находятся в среде во взвешенном состоянии.

2. Открытие броуновского движения

2.1. Наблюдение

Это явление открыто Р. Броуном в 1827 году, когда он проводил исследования пыльцы растений . Шотландский ботаник Роберт Броун (иногда его фамилию транскрибируют как Браун) ещё при жизни как лучший знаток растений получил титул «князя ботаников». Он сделал много замечательных открытий. В 1805 после четырёхлетней экспедиции в Австралию привез в Англию около 4000 видов не известных ученым австралийских растений и много лет потратил на их изучение. Описал растения, привезенные из Индонезии и Центральной Африки. Изучал физиологию растений, впервые подробно описал ядро растительной клетки. Петербургская Академия наук сделала его своим почетным членом. Но имя учёного сейчас широко известно вовсе не из-за этих работ.

В Викитеке есть полный текст A brief account of microscopical observations made on the particles contained in the pollen of plants

В 1827 Броун проводил исследования пыльцы растений. Он, в частности, интересовался, как пыльца участвует в процессе оплодотворения. Как-то он разглядывал под микроскопом выделенные из клеток пыльцы североамериканского растения Clarkia pulchella (кларкии хорошенькой) взвешенные в воде удлиненные цитоплазматические зерна. Неожиданно Броун увидел, что мельчайшие твёрдые крупинки, которые едва можно было разглядеть в капле воды, непрерывно дрожат и передвигаются с места на место. Он установил, что эти движения, по его словам, «не связаны ни с потоками в жидкости, ни с ее постепенным испарением, а присущи самим частичкам».

Наблюдение Броуна подтвердили другие учёные. Мельчайшие частички вели себя, как живые, причем «танец» частиц ускорялся с повышением температуры и с уменьшением размера частиц и явно замедлялся при замене воды более вязкой средой. Это удивительное явление никогда не прекращалось: его можно было наблюдать сколь угодно долго. Поначалу Броун подумал даже, что в поле микроскопа действительно попали живые существа, тем более что пыльца – это мужские половые клетки растений, однако так же вели частички из мертвых растений, даже из засушенных за сто лет до этого в гербариях. Тогда Броун подумал, не есть ли это «элементарные молекулы живых существ», о которых говорил знаменитый французский естествоиспытатель Жорж Бюффон (1707–1788), автор 36-томной Естественной истории. Это предположение отпало, когда Броун начал исследовать явно неживые объекты; сначала это были очень мелкие частички угля, а также сажи и пыли лондонского воздуха, затем тонко растертые неорганические вещества: стекло, множество различных минералов. «Активные молекулы» оказались повсюду: «В каждом минерале, – писал Броун, – который мне удавалось измельчить в пыль до такой степени, чтобы она могла в течение какого-то времени быть взвешенной в воде, я находил, в больших или меньших количествах, эти молекулы».

Надо сказать, что у Броуна не было каких-то новейших микроскопов. В своей статье он специально подчеркивает, что у него были обычные двояковыпуклые линзы, которыми он пользовался в течение нескольких лет. И далее пишет: «В ходе всего исследования я продолжал использовать те же линзы, с которыми начал работу, чтобы придать больше убедительности моим утверждениям и чтобы сделать их как можно более доступными для обычных наблюдений».

Сейчас, чтобы повторить наблюдение Броуна, достаточно иметь не очень сильный микроскоп и рассмотреть с его помощью дым в зачерненной коробочке, освещенный через боковое отверстие лучом интенсивного света. В газе явление проявляется значительно ярче, чем в жидкости: видны рассеивающие свет маленькие клочки пепла или сажи (в зависимости от источника дыма), которые непрерывно скачут туда и сюда. Удается наблюдать броуновское движение и в растворе туши: при увеличении 400 х движение частиц уже легко различимо.

Как это часто бывает в науке, спустя многие годы историки обнаружили, что ещё в 1670 изобретатель микроскопа голландец Антони Левенгук, видимо, наблюдал аналогичное явление, но редкость и несовершенство микроскопов, зачаточное состояние молекулярного учения в то время не привлекли внимания к наблюдению Левенгука, поэтому открытие справедливо приписывают Броуну, который впервые подробно его изучил и описал.

3. Теория броуновского движения

3.1. Построение классической теории

В 1905 году Альбертом Эйнштейном была создана молекулярно-кинетическая теория для количественного описания броуновского движения. :13 В частности, он вывел формулу для коэффициента диффузии сферических броуновских частиц :

где D - коэффициент диффузии, R - универсальная газовая постоянная, T - абсолютная температура, N A - постоянная Авогадро, a - радиус частиц, ξ - динамическая вязкость.

3.2. Экспериментальное подтверждение

Формула Эйнштейна была подтверждена опытами Жана Перрена :13 и его студентов в 1908-1909 гг. В качестве броуновских частиц они использовали зёрнышки смолы мастикового дерева и гуммигута - густого млечного сока деревьев рода гарциния . Справедливость формулы была установлена для различных размеров частиц - от 0,212 мкм до 5,5 мкм, для различных растворов (раствор сахара, глицерин), в которых двигались частицы :109-133 .

3.3. Броуновское движение как немарковский случайный процесс

Хорошо разработанная за последнее столетие теория броуновского движения является приближенной. И хотя в большинстве практически важных случаев существующая теория даёт удовлетворительные результаты, в некоторых случаях она может потребовать уточнения. Так, экспериментальные работы, проведённые в начале XXI века в Политехническом университете Лозанны, Университете Техаса и Европейской молекулярно-биологической лаборатории в Гейдельберге (под руководством С. Дженей) показали отличие поведения броуновской частицы от теоретически предсказываемого теорией Эйнштейна - Смолуховского, что было особенно заметным при увеличении размеров частиц. Исследования затрагивали также анализ движения окружающих частиц среды и показали существенное взаимное влияние движения броуновской частицы и вызываемое ею движение частиц среды друг на друга, то есть наличие «памяти» у броуновской частицы, или, другими словами, зависимость её статистических характеристик в будущем от всей предыстории её поведения в прошлом. Данный факт не учитывался в теории Эйнштейна - Смолуховского.

Процесс броуновского движения частицы в вязкой среде, вообще говоря, относится к классу немарковских процессов, и для более точного его описания необходимо использование интегральных стохастических уравнений .

Примечания

Броуновское движение - ru.wikisource.org/wiki/ЭСБЕ/Броуновское_движение // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). - СПб. , 1890-1907.
1 2 Б.Б.Буховцев, Ю.Л.Климонтович, Г.Я.Мякишев Физика. Учебник для 9 класса средней школы. - 3 изд., переработанное. - М .: Просвещение, 1986. - 3210000 экз .
Einstein, Albert (May 1905). «Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen - www.physik.uni-augsburg.de/theo1/hanggi/History/Einstein1905BMI.pdf» (PDF). Annalen der Physik 322 (8): 549–560. DOI:10.1002/andp.19053220806 - dx.doi.org/10.1002/andp.19053220806. Проверено 2010-09-21. (нем.) ,
перевод на русский:Эйнштейн, А. О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты - www.mirgorodsky.ru/mirgorodskiyal_statya/O_DVIGENII_VZVESHENNIH_V_POKOJASCHEISYA_JZIDKOSTI_CHASTITC_EINSHTEIN_1905.pdf // Броуновское движение.А.Эйнштейн, М. Смолуховский. Сб. ст. [пер. с нем. и франц.] . - М.-Л: ОНТИ, 1936.
Гуммигут - slovari.yandex.ru/~книги/БСЭ/Гуммигут/ в БСЭ
Perrin, J. Atoms - www.archive.org/stream/atomsper00perruoft. - London: Constable & Company, 1916. ,
один из самых ранних переводов на русский: Перрен, Ж. Атомы. - М .: Госиздат, 1921. - 254 с. - (Современные проблемы естествознания).
Morozov A.N., Skripkin A.V. Application of integral transforms to a description of the Brownian motion by a non-Markovian random process // Russian Physics Journal. 2009. Volume 52, Number 2, 184-195 - www.springerlink.com/content/wt37k3402658w044/
Морозов А.Н., Скрипкин А.В. Применение интегральных преобразований для описания броуновского движения как немарковского случайного процесса // Известия вузов. Физика. 2009. №2. С. 66 – 74

«Физика - 10 класс»

Вспомните из курса физики основной школы явление диффузии.
Чем может быть объяснено это явление?

Ранее вы узнали, что такое диффузия , т. е. проникновение молекул одного вещества в межмолекулярное пространство другого вещества. Это явление определяется беспорядочным движением молекул. Этим можно объяснить, например, тот факт, что объём смеси воды и спирта меньше объёма составляющих её компонентов.

Но самое очевидное доказательство движения молекул можно получить, наблюдая в микроскоп мельчайшие, взвешенные в воде частицы какого-либо твёрдого вещества. Эти частицы совершают беспорядочное движение, которое называют броуновским .

Броуновское движение - это тепловое движение взвешенных в жидкости (или газе) частиц.

Наблюдение броуновского движения.

Английский ботаник Р. Броун (1773-1858) впервые наблюдал это явление в 1827 г., рассматривая в микроскоп взвешенные в воде споры плауна.

Позже он рассматривал и другие мелкие частицы, в том числе частички камня из египетских пирамид. Сейчас для наблюдения броуновского движения используют частички краски гуммигут, которая нерастворима в воде. Эти частички совершают беспорядочное движение. Самым поразительным и непривычным для нас является то, что это движение никогда не прекращается. Мы ведь привыкли к тому, что любое движущееся тело рано или поздно останавливается. Броун вначале думал, что споры плауна проявляют признаки жизни.

Броуновское движение - тепловое движение, и оно не может прекратиться. С увеличением температуры интенсивность его растёт.

На рисунке 8.3 приведены траектории движения броуновских частиц. Положения частиц, отмеченные точками, определены через равные промежутки времени - 30 с. Эти точки соединены прямыми линиями. В действительности траектория частиц гораздо сложнее.

Объяснение броуновского движения.

Объяснить броуновское движение можно только на основе молекулярно-кинетической теории.

«Немногие явления способны так увлечь наблюдателя, как броуновское движение. Здесь наблюдателю позволяется заглянуть за кулисы того, что совершается в природе. Перед ним открывается новый мир - безостановочная сутолока огромного числа частиц. Быстро пролетают в поле зрения микроскопа мельчайшие частицы, почти мгновенно меняя направление движения. Медленнее продвигаются более крупные частицы, но и они постоянно меняют направление движения. Большие частицы практически толкутся на месте. Их выступы явно показывают вращение частиц вокруг своей оси, которая постоянно меняет направление в пространстве. Нигде нет и следа системы или порядка. Господство слепого случая - вот какое сильное, подавляющее впечатление производит эта картина на наблюдателя». R. Поль (1884-1976).

Причина броуновского движения частицы заключается в том, что удары молекул жидкости о частицу не компенсируют друг друга.

На рисунке 8.4 схематически показано положение одной броуновской частицы и ближайших к ней молекул.

При беспорядочном движении молекул передаваемые ими броуновской частице импульсы, например слева и справа, неодинаковы. Поэтому отлична от нуля результирующая сила давления молекул жидкости на броуновскую частицу. Эта сила и вызывает изменение движения частицы.

Молекулярно-кинетическая теория броуновского движения была создана в 1905 г. А. Эйнштейном (1879-1955). Построение теории броуновского движения и её экспериментальное подтверждение французским физиком Ж. Перреном окончательно завершили победу молекулярно-кинетической теории. В 1926 г. Ж. Перрен получил Нобелевскую премию за исследование структуры вещества.

Опыты Перрена.

Идея опытов Перрена состоит в следующем. Известно, что концентрация молекул газа в атмосфере уменьшается с высотой. Если бы не было теплового движения, то все молекулы упали бы на Землю и атмосфера исчезла бы. Однако если бы не было притяжения к Земле то за счёт теплового движения молекулы покидали бы Землю, так как газ способен к неограниченному расширению. В результате действия этих противоположных факторов устанавливается определённое распределение молекул по высоте, т. е. концентрация молекул довольно быстро уменьшается с высотой. Причём чем больше масса молекул, тем быстрее с высотой убывает их концентрация.

Броуновские частицы участвуют в тепловом движении. Так как их взаимодействие пренебрежимо мало, то совокупность этих частиц в газе или жидкости можно рассматривать как идеальный газ из очень тяжёлых молекул. Следовательно, концентрация броуновских частиц в газе или жидкости в поле тяжести Земли должна убывать по тому же закону, что и концентрация молекул газа. Закон этот известен.

Перрен с помощью микроскопа большого увеличения и малой глубины поля зрения (малой глубины резкости) наблюдал броуновские частицы в очень тонких слоях жидкости. Подсчитывая концентрацию частиц на разных высотах, он нашёл, что эта концентрация убывает с высотой по тому же закону, что и концентрация молекул газа. Отличие в том, что за счёт большой массы броуновских частиц убывание происходит очень быстро.

Все эти факты свидетельствуют о правильности теории броуновского движения и о том, что броуновские частицы участвуют в тепловом движении молекул.

Подсчёт броуновских частиц на разных высотах позволил Перрену определить постоянную Авогадро совершенно новым методом. Значение этой постоянной совпало с ранее известным.

Одним из наиболее убедительных доказательств реальности движения молекул служит явление так называемого броуновского движения, открытого в 1827 г. английским ботаником Броуном при изучении взвешенных в воде мельчайших спор. Он обнаружил, при рассмотрении под микроскопом с большим увеличением, что эти споры находятся в непрерывном беспорядочном движении, как бы исполняя дикий фантастический танец.

Дальнейшие опыты показали, что эти движения не связаны с биологическим происхождением частиц или с какими-либо движениями жидкости. Подобные движения совершают любые малые частицы, взвешенные в жидкости или газе. Такого рода беспорядочные движения совершают, например, частицы дыма в неподвижном воздухе. Такое беспорядочное движение частиц, взвешенных в жидкости или газе, и получило название броуновского движения.

Специальные исследования показали, что характер броуновского движения зависит от свойств жидкости или газа, в которых взвешены частицы, но не зависит от свойств вещества самих частиц. Скорость движения броуновских частиц возрастает с повышением температуры и с уменьшением размеров частиц.

Все эти закономерности легко объяснить, если мы примем, что движения взвешенных частиц возникают вследствие ударов, испытываемых ими со стороны движущихся молекул жидкости или газа, в которых они находятся.

Конечно, каждая броуновская частица подвергается таким ударам со всех сторон. При полной беспорядочности молекулярных движений можно, казалось бы, ожидать, что число ударов, обрушивающихся на частицу с какого-нибудь направления, должно быть в точности равно числу ударов с противоположного направления,

так что все эти толчки должны полностью компенсировать друг друга и частицы должны оставаться неподвижными.

Так именно и происходит, если частицы не слишком малы. Но когда мы имеем дело с микроскопическими частицами см), дело обстоит иначе. Ведь из того факта, что молекулярные движения хаотичны, следует лишь, что в среднем число ударов разных направлений одинаково. Но в такой статистической системе, как жидкость или газ, неизбежны и отклонения от средних значений. Такие отклонения от средних значений тех или иных величин, которые происходят в малом объеме или в течение малых промежутков времени, называются флуктуациями. Если в жидкости или газе находится тело обычных размеров, то число толчков, которое оно испытывает со стороны молекул, так велико, что нельзя заметить ни отдельных толчков, ни случайного преобладания толчков одного направления над толчками других направлений. Для малых же частиц общее число испытываемых ими толчков сравнительно невелико, так что преобладание числа ударов то одного, то другого направления становится заметным, и именно благодаря таким флуктуациям числа ударов и возникают те характерные, как бы судорожные движения взвешенных частиц, которые и называются броуновским движением.

Ясно, что движения броуновских частиц - это не молекулярные движения: мы видим не результат удара одной молекулы, а результат преобладания числа ударов одного направления над числом ударов в противоположном направлении. Броуновское движение лишь очень ясно обнаруживает само существование беспорядочных молекулярных движений.

Таким образом, броуновское движение объясняется тем, что благодаря случайной неодинаковости чисел ударов молекул о частицу с разных направлений возникает некоторая равнодействующая сила определенного направления. Так как флуктуации обычно бывают кратковременными, то через короткий промежуток времени направление равнодействующей изменится, а вместе с ней изменится и направление перемещения частицы. Отсюда наблюдающаяся хаотичность броуновских движений, отражающая хаотичность молекулярного движения.

Приведенное качественное объяснение броуновского движения мы теперь дополним количественным рассмотрением этого явления. Количественная теория его была впервые дана Эйнштейном и, независимо, Смолуховским (1905 г.). Мы приведем здесь более простой, чем у этих авторов, вывод основного соотношения этой теории.

Вследствие неполной компенсации ударов молекул на броуновскую частицу действует, как мы видели, некоторая результирующая сила под действием которой частица и движется. Кроме этой силы на частицу действует сила трения вызванная вязкостью среды и направленная против силы

Для простоты предположим, что частица имеет форму сферы радиуса а. Тогда сила трения может быть выражена формулой Стокса:

где коэффициент внутреннего трения жидкости (или газа), скорость движения частицы. Уравнение движения частицы (второй закон Ньютона) имеет поэтому вид:

Здесь масса частицы, ее радиус-вектор относительно произвольной системы координат, скорость частицы и равнодействующая сил, вызванных ударами молекул.

Рассмотрим проекцию радиуса-вектора на одну из координатных осей, например на ось Для этой составляющей уравнение (7,1) перепишется в виде:

где составляющая результирующей силы по оси

Наша задача состоит в том, чтобы найти смещение х броуновской частицы, которое она получает под действием ударов молекул. Каждая из частиц все время подвергается соударениям с молекулами, после чего она меняет направление своего движения. Различные частицы получают смещения, отличающиеся как по величине, так и по направлению. Вероятное значение суммы смещений всех частиц равно нулю, так как смещения с равной вероятностью могут иметь и положительный, и отрицательный знак. Среднее значение проекции смещения частиц х будет поэтому равно нулю. Не будет, однако, равно нулю среднее значение квадрата смещения, т. е. величина хтак как не изменяет своего знака при изменении знака х. Преобразуем поэтому уравнение (7.2) так, чтобы в него входила величина Для этого умножим обе части этого уравнения на

Используем очевидные тождества:

Подставив эти выражения в (7.3), получим:

Это равенство справедливо для любой частицы и поэтому оно справедливо также и для средних значений входящих в него величин,

если усреднение вести по достаточно большому числу частиц. Поэтому можно написать:

где среднее значение квадрата перемещения частицы, среднее значение квадрата ее скорости. Что касается среднего значения величины входящей в равенство, то оно равно нулю, так как для большого числа частиц одинаково часто принимают как положительные, так и отрицательные значения. Уравнение (7.2) прикимает поэтому вид:

Величина в этом уравнении представляет собой среднее значение квадрата проекций скорости на ось Так как движения частиц вполне хаотичны, то средние значения квадратов проекций скорости по всем трем координатным осям должны быть равны друг другу, т. е.

Очевидно также, что сумма этих величин должна быть равна среднему значению квадрата скорости частиц

Следовательно,

Таким образом, интересующее нас выражение, входящее в (7.4), равно:

Величина есть средняя кинетическая энергия броуновской частицы. Сталкиваясь с молекулами жидкости или газа, броуновские частицы обмениваются с ними энергией и находятся в тепловом равновесии со средой, в которой они движутся. Поэтому средняя кинетическая энергия поступательного движения броуновской частицы должна быть равна средней кинетической энергии молекул

жидкости (или газа), которая, как мы знаем, равна

и следовательно

То обстоятельство, что средняя кинетическая энергия броуновской частицы равна (как и для газовой молекулы!), имеет принципиальное значение. Действительно, выведенное нами ранее основное уравнение (3.1) справедливо для любых не взаимодействующих друг с другом частиц, совершающих хаотические движения. Будут ли это невидимые глазом молекулы или значительно более крупные броуновские частицы, содержащие миллиарды молекул, - безразлично. С молекулярно-кинетической точки зрения броуновскую частицу можно трактовать как гигантскую молекулу. Поэтому выражение для средней кинетической энергии такой частицы должно быть таким же, как и для молекулы. Скорости же броуновских частиц, конечно, несравненно меньше, соответственно их большей массе.

Вернемся теперь к уравнению (7.4) и, учтя (7.5), перепишем его

Это уравнение легко интегрируется. Обозначив получаем:

и после разделения переменных наше уравнение преобразуется в виде:

Интегрируя левую часть этого уравнения в пределах от 0 до а правую от до получаем:

Величина как легко убедиться, в обычных условиях опыта ничтожно мала. Действительно, размеры броуновских частиц не превышают см, вязкость жидкости обычно близка к вязкости воды, т. е. приблизительно равна (в системе единиц плотность вещества частиц порядка единицы, Имея в виду, что масса частицы равна , мы получим, что показатель степени при таков, что величиной можно пренебречь. Следовательно, если отрезок времени между последовательными наблюдениями за броуновской частицей превышает что, конечно, всегда имеет место, то

Для конечных промежутков времени и соответствующих перемещений уравнение (7.6) можно переписать в виде:

Среднее значение квадрата смещения броуновской частицы за промежуток времени вдоль оси X, или любой другой оси, пропорционально этому промежутку времени.

Формула (7.7) позволяет вычислять среднее значение квадрата перемещений, причем среднее берется по всем частицам, участвующим в явлении. Но эта формула справедлива и для среднего значения квадрата многих последовательных перемещений одной-единственной частицы за равные промежутки времени, С экспериментальной точки зрения удобнее наблюдать именно перемещения одной частицы. Такие наблюдения и были проведены Перреном в 1909 г.

Движение частиц Перрен наблюдал через микроскоп, окуляр которого был снабжен сеткой взаимно перпендикулярных линий, служивших координатной системой. Пользуясь сеткой, Перрен отмечал на ней последовательные положения одной облюбованной им частицы через определенные промежутки времени (например, 30 с). Соединив затем точки, отмечающие положения частицы на сетке, он получил картину, подобную той, которая изображена на рис, 7. На этом рисунке показаны как смещения частицы, так и их проекции на ось

Следует иметь в виду, что движения частицы значительно сложнее, чем об этом можно судить по рис. 7, так как здесь отмечены положения через не слишком малые промежутки времени (порядка 30 с). Если уменьшить эти промежутки, то окажется, что каждый прямолинейный отрезок на рисунке развернется в такую же сложную зигзагообразнуютраекторию, как и весь рис. 7.

Так как постоянная может быть определена из уравнения сестояния.

Опыты Перрена имели большое значение для окончательного обоснования молекулярно-кинетической теории.

Броуновским движением называют беспорядочное (хаотичное) движение твердых очень мелких частиц, взвешенных в жидкости или газе. Но что заставляет твердые частицы двигаться?

В XIX веке подобное явление впервые описал ученый-ботаник Р. Броун (в честь него было названо это явление). Он наблюдал, как в воде беспорядочно металась пыльца, затем сажа. Но объяснить это явление он не мог.

Позже ученые предположили, что хаотичное движение мельчайших частиц может возникать из-за ударов по ним молекул жидкости или газа, в которых они находятся. Это предположение возникло не на пустом месте. Было замечено, что чем мельче частицы твердого вещества, тем быстрее они движутся в воде. Это наводит на мысль, что их что-то толкает. И чем частицы крупнее, тем их труднее толкать, и поэтому крупные двигаются медленнее.

В начале XX века эта гипотеза подтвердилась.

Таким образом броуновское движение частиц доказывает

молекулярное строение вещества ,
то, что молекулы двигаются .

Следует не путать броуновское движение с движением молекул. Броуновское движение частиц, взвешенных в жидкости или газе, является следствием движения молекул этих жидкости или газа.

Молекул жидкости или газа очень много. Все они двигаются хаотически. Поэтому толкают броуновскую частицу с разных сторон. Следовательно, сама частица тоже начинает двигаться хаотически.

Изучение броуновского движения также помогло открыть то, что с повышением температуры скорость движения молекул возрастает . Этот факт следовал из того, что с увеличением температуры увеличивалась интенсивность броуновского движения. Значит, по частицам вещества молекулы среды, где они находились, ударяли сильнее.

По причине зависимости от температуры движение молекул также называют тепловым движением .

Скорость, с которой двигаются молекулы, огромна. Она измеряется сотнями метров в секунду. Так как молекулы очень мелкие, и «бьют» по телам они очень часто, то для крупных тел эти удары воспринимаются как давление среды (воды, воздуха).

На видео ниже записано реальное броуновское движение наночастиц в воде. Так оно выглядит под оптическим микроскопом.

Что такое Броуновское движение

Это движение характеризуется следующими чертами:

продолжается неограниченно долго без каких бы то ни было видимых изменений,
интенсивность движения броуновских частиц зависит от их размеров, но не зависит от их природы,
интенсивность возрастает с ростом температуры,
интенсивность возрастает с уменьшением вязкости жидкости или газа.

Броуновское движение не является молекулярным движением, но служит непосредственным доказательством существования молекул и хаотического характера их теплового движения.

Сущность Броуновского движения

Сущность этого движения в следующем. Частица вместе с молекулами жидкости или газа образуют одну статистическую систему. В соответствии с теоремой о равномерном распределении энергии по степени свободы на каждую степень свободы приходится 1/2kT энергии. Энергия 2/3kT, приходящаяся на три поступательные степени свободы частицы, приводит к движению ее центра масс, которое наблюдается под микроскопом в виде дрожания частицы. Если броуновская частица достаточно жесткая, то еще 3/2kT энергии приходится на ее вращательные степени свободы. Поэтому при своем дрожании она испытывает еще и постоянные изменения ориентировки в пространстве.

Можно объяснить броуновское движение и так: причиной Броуновского движения являются флуктуации давления, которое оказывается на поверхность малой частицы со стороны молекул среды. Сила и давление изменяется по модулю и направлению, в результате чего частица находится в беспорядочном движении.

Движение броуновской частицы является случайным процессом. Вероятность (dw) того, что броуновская частица, находившаяся в однородной изотропной среде в начальный момент времени (t=0) в начале координат, сместится вдоль произвольно направленной (при t$>$0) оси Ox так, что ее координата будет лежать в интервале от x до x+dx, равна:

где $\triangle x$- малое изменение координаты частицы, вследствие флуктуации.

Рассмотрим положение Броуновской частицы через некоторые фиксированные промежутки времени. Начало координат поместим в точку, в которой частица находилась при t=0. Обозначим $\overrightarrow{q_i}$ -- вектор , который характеризует перемещение частицы между (i-1) и i наблюдениями. По истечении n наблюдений частица сместится из нулевого положения в точку с радиус-вектором $\overrightarrow{r_n}$. При этом:

\[\overrightarrow{r_n}=\sum\limits^n_{i=1}{\overrightarrow{q_i}}\left(2\right).\]

Перемещения частицы происходит по сложной ломаной линии все время наблюдений.

Найдем средний квадрат удаления частицы от начала после n шагов в большой серии опытов:

\[\left\langle r^2_n\right\rangle =\left\langle \sum\limits^n_{i,j=1}{q_iq_j}\right\rangle =\sum\limits^n_{i=1}{\left\langle {q_i}^2\right\rangle }+\sum\limits^n_{i\ne j}{\left\langle q_iq_j\right\rangle }\left(3\right)\]

где $\left\langle q^2_i\right\rangle $- средний квадрат смещения частицы на i- м шаге в серии опытов (он для всех шагов одинаков и равен какой-то положительной величине a2), $\left\langle q_iq_j\right\rangle $- является средней величиной скалярного произведения при i-м шаге на перемещение при j-м шаге в различных опытах. Эти величины независимы друг от друга, одинаково часто встречаются как положительные значения скалярного произведения, так и отрицательные. Поэтому, считаем, что $\left\langle q_iq_j\right\rangle $=0 при$\ i\ne j$. Тогда имеем из (3):

\[\left\langle r^2_n\right\rangle =a^2n=\frac{a^2}{\triangle t}t=\alpha t=\left\langle r^2\right\rangle \left(4\right),\]

где $\triangle t$- промежуток времени между наблюдениями; t=$\triangle tn$ - время, в течение которого средний квадрат удаления частицы стал равен $\left\langle r^2\right\rangle .$ Получаем, что частица удаляется от начала. Существенно то, что средний квадрат удаления растет пропорционально первой степени времени. $\alpha \ $- можно найти экспериментально, а можно теоретически, как будет показано в примере 1.

Броуновская частица движется не только поступательно, но и вращаясь. Среднее значение угла поворота $\triangle \varphi $ броуновской частицы за время t равно:

\[{\triangle \varphi }^2=2D_{vr}t(5),\]

где $D_{vr}$ -- коэффициент вращательной диффузии. Для сферической броуновской частицы радиуса - а $D_{vr}\ $ равен:

где $\eta $ - коэффициент вязкости среды.

Броуновское движение ограничивает точность измерительных приборов. Предел точности зеркального гальванометра определяется дрожание зеркальца, подобно броуновской частице, которая подвергается ударам молекул воздуха. Случайное движение электронов вызывает шумы в электрических сетях.

Пример 1

Задание: Для того, чтобы математически полно охарактеризовать броуновское движение, надо найти $\alpha $ в формуле $\left\langle r^2_n\right\rangle =\alpha t$. Считать коэффициент вязкости жидкости известным и равным b, температура жидкости T.

Запишем уравнение движения броуновской частицы в проекции на ось Ox:

где m -- масса частицы, $F_x$ -- случайная сила, действующая на частицу, $b\dot{x}$- член уравнения, характеризующий силу трения, действующая на частицу в жидкости.

Аналогичный вид имеют уравнения для величин, относящиеся к другим координатным осям.

Умножим обе части уравнения (1.1) на x, а члены $\ddot{x}x\ и\ \dot{x}x$ преобразуем:

\[\ddot{x}x=\ddot{\left(\frac{x^2}{2}\right)}-(\dot{x})^2,\dot{x}x=(\frac{x^2}{2}\)(1.2)\]

Тогда уравнение (1.1) приведем к виду:

\[\frac{m}{2}(\ddot{x^2})-m(\dot{x})^2=-\frac{b}{2}\left(\dot{x^2}\right)+F_xx\ (1.3)\]

Усредним обе части этого уравнения по ансамблю броуновских частиц, учитывая при этом, что средняя от производной по времени равна производной от средней величины, так как это усреднение по ансамблю частиц, и, значит, переставим операцией дифференцирования по времени. В результате усреднения (1.3) получаем:

\[\frac{m}{2}\left(\left\langle \ddot{x^2}\right\rangle \right)-\left\langle m(\dot{x})^2\right\rangle =-\frac{b}{2}\left(\dot{\left\langle x^2\right\rangle }\right)+\left\langle F_xx\right\rangle \ \left(1.4\right).\]

Так как отклонения броуновской частицы в любом направлении равновероятны, то:

\[\left\langle x^2\right\rangle =\left\langle y^2\right\rangle =\left\langle z^2\right\rangle =\frac{\left\langle r^2\right\rangle }{3}\left(1.5\right)\]

Используем $\left\langle r^2_n\right\rangle =a^2n=\frac{a^2}{\triangle t}t=\alpha t=\left\langle r^2\right\rangle $, получаем $\left\langle x^2\right\rangle =\frac{\alpha t}{3}$, следовательно: $\dot{\left\langle x^2\right\rangle }=\frac{\alpha }{3}$, $\left\langle \ddot{x^2}\right\rangle =0$

Из-за случайного характера силы $F_x$ и координаты частицы x и их независимости друг от друга должно выполняться равенство $\left\langle F_xx\right\rangle =0$, тогда (1.5) сводится к равенству:

\[\left\langle m{\dot{\left(x\right)}}^2\right\rangle =\frac{\alpha b}{6}\left(1.6\right).\]

По теореме о равномерном распределении энергии по степеням свободы:

\[\left\langle m{\dot{\left(x\right)}}^2\right\rangle =kT\left(1.7\right).\] \[\frac{\alpha b}{6}=kT\to \alpha =\frac{6kT}{b}.\]

Таким образом, получим формулу для решения задачи о Броуновском движении:

\[\left\langle r^2\right\rangle =\frac{6kT}{b}t\]

Ответ: Формула $\left\langle r^2\right\rangle =\frac{6kT}{b}t$ решает задачу о броуновском движении взвешенных частиц.

Пример 2

Задание: Частицы гуммигута сферической формы радиуса r участвуют в броуновском движении в газе. Плотность гуммигута $\rho $. Найти среднеквадратичную скорость частиц гуммигута при температуре T.

Среднеквадратичная скорость молекул равна:

\[\left\langle v^2\right\rangle =\sqrt{\frac{3kT}{m_0}}\left(2.1\right)\]

Броуновская частица находится в равновесии с веществом, в котором она находится, и мы можем рассчитать ее среднеквадратичную скорость, используя формулу для скорости молекул газа, которые, в свою очередь, двигаясь, заставляют перемещаться броуновскую частицу. Для начала найдем массу частицы:

\[\left\langle v^2\right\rangle =\sqrt{\frac{9kT}{4\pi R^3\rho }}\]

Ответ: Скорость частицы гуммигута взвешенного в газе можно найти как $\left\langle v^2\right\rangle =\sqrt{\frac{9kT}{4\pi R^3\rho }}$.