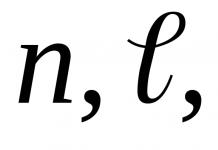Ранг матрицы: определение, методы нахождения, примеры, решения. Ранг матрицы Ранг единичной матрицы

Ранее для квадратной матрицы -го порядка было введено понятие минора
элемента. Напомним, что так был назван определитель порядка
, полученный из определителя
вычеркиванием-й строки и-го столбца.

Введем теперь общее понятие минора. Рассмотрим некоторую, не обязательно квадратную матрицу . Выберем какие-нибудьномеров строк
иномеров столбцов
.

Определение . Минором порядка матрицы (соответствующим выбранным строкам и столбцам) называется определитель порядка, образованный элементами, стоящими на пересечении выбранных строк и столбцов, т.е. число

.

Каждая матрица имеет столько миноров данного порядка , сколькими способами можно выбрать номера строк
и столбцов
.

Определение . В матрице размеров
минор порядканазываетсябазисным , если он отличен от нуля, а все миноры порядка
равны нулю или миноров порядка
у матрицывообще нет.

Ясно, что в матрице может быть несколько разных базисных миноров, но все базисные миноры имеют один и тот же порядок. Действительно, если все миноры порядка
равны нулю, то равны нулю и все миноры порядка
, а, следовательно, и всех бόльших порядков.

Определение . Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если все элементы матрицы равны нулю, то ранг такой матрицы, по определению, считают нулем.

Ранг матрицы будем обозначать символом
. Из определения ранга следует, что для матрицыразмеров
справедливо соотношение.

Два способа вычисления ранга матрицы

а) Метод окаймляющих миноров

Пусть в матрице найден минор
-го порядка, отличный от нуля. Рассмотрим лишь те миноры
-го порядка, которые содержат в себе (окаймляют) минор
: если все они равны нулю, то ранг матрицы равен. В противном случае среди окаймляющих миноров найдется ненулевой минор
-го порядка, и вся процедура повторяется.

Пример 9 . Найти ранг матрицы методом окаймляющих миноров.

Выберем минор второго порядка
. Существует только один минор третьего порядка, окаймляющий выбранный минор
. Вычислим его.

Значит, минор
базисный, а ранг матрицы равен его порядку, т.е.

Ясно, что перебирать таким способом миноры в поисках базисного – задача, связанная с большими вычислениями, если размеры матрицы не очень малы. Существует, однако, более простой способ нахождения ранга матрицы – при помощи элементарных преобразований.

б) Метод элементарных преобразований

Определение . Элементарными преобразованиями матрицы называют следующие преобразования:

умножение строки на число, отличное от нуля;

прибавление к одной строке другой строки;

перестановку строк;

такие же преобразования столбцов.

Преобразования 1 и 2 выполняются поэлементно.

Комбинируя преобразования первого и второго вида, мы можем к любой строке прибавить линейную комбинацию остальных строк.

Теорема . Элементарные преобразования не меняют ранга матрицы.

(Без доказательства)

Идея практического метода вычисления ранга матрицы

заключается в том, что с помощью элементарных преобразований данную матрицу приводят к виду

, (5)

в котором «диагональные» элементы
отличны от нуля, а элементы, расположенные ниже «диагональных», равны нулю. Условимся называть матрицутакого вида треугольной (иначе, ее называют диагональной, трапециевидной или лестничной). После приведения матрицык треугольному виду можно сразу записать, что
.

В самом деле,
(т.к. элементарные преобразования не меняют ранга). Но у матрицысуществует отличный от нуля минор порядка:

,

а любой минор порядка
содержит нулевую строку и поэтому равен нулю.

Сформулируем теперь практическое правило вычисления ранга матрицы с помощью элементарных преобразований: для нахождения ранга матрицыследует с помощью элементарных преобразований привести ее к треугольному виду. Тогда ранг матрицыбудет равен числу ненулевых строк в полученной матрице.

Пример 10. Найти ранг матрицы методом элементарных преобразований

Решение.

Поменяем местами первую и вторую строку (т.к. первый элемент второй строки −1 и с ней будет удобно выполнять преобразования). В результате получим матрицу, эквивалентную данной.

Обозначим -тую строку матрицы –. Нам необходимо привести исходную матрицу к треугольному виду. Первую строку будем считать ведущей, она будет участвовать во всех преобразованиях, но сама остается без изменений.

На первом этапе выполним преобразования, позволяющие получить в первом столбце нули, кроме первого элемента. Для этого из второй строки вычтем первую, умноженную на 2
, к третьей строке прибавим первую
, а из третьей вычтем первую, умноженную на 3
Получаем матрицу, ранг которой совпадает с рангом данной матрицы. Обозначим ее той же буквой:

.

Так как нам необходимо привести матрицу к виду (5), вычтем из четвертой строки вторую. При этом имеем:

.

Получена матрица треугольного вида, и можно сделать вывод, что
, т. е. числу ненулевых строк. Коротко решение задачи можно записать следующим образом:

Рассмотрим матрицу А размера .

А=
Выделим в нейkстрок иkстолбцов (
).

Определение 26: Минором k-го порядка матрицы А называется определитель квадратной матрицы, получающийся из данной выделением в ней.

kстрок иkстолбцов.

Определение 27: Рангом матрицы называется наибольший из порядков, отличных от нуля, ее миноров,r(A).

Определение 28: Минор, порядок которого совпадает с рангом называетсябазисным минором .

Утверждение:

1. Ранг выражается целым числом.(
)

2. r=0,
, когда А – нулевая.

Элементарные преобразования матриц.

К элементарным преобразованиям матриц относятся следующие:

1) умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число.

2) прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца) умноженные на одно и то же число;

3) перестановка местами строк (столбцов) матрицы;

4) отбрасывание нулевой строки (столбца);

5) замена строк матрицы соответствующими столбцами.

Определение 29: Матрицы, получающиеся одна из другой, при элементарных преобразованиях называется эквивалентными матрицами, обозначаются “ ~“

Основное свойство эквивалентных матриц: Ранги эквивалентных матриц равны.

Пример 18: Вычислитьr(A),

Решение: Первую строку умножим поэтапно на (-4)(-2)

(-7) и затем прибавим соответственно к второй, третьей и четвертой строкам.

~

поменяем местами вторую и четвертую строки
вторую строку умножим на (-2) и прибавим к четвертой строке; сложим вторую и третью строки.

сложим третью и четвертую строки.

~
откинем нулевую строку

~
r(A)=3
ранг исходной матрицы

равен трем.

Определение 30: Назовем матрицу А ступенчатой, если все элементы главной диагонали0, а элементы под главной диагональю равны нулю.

Предложение :

1) ранг ступенчатой матрицы равен числу ее строк;

2) всякая матрица может быть приведена к ступенчатому виду с помощью элементарных преобразований.

Пример 19: При каких значениях  матрица
имеет ранг, равный единице?

Решение: Ранг равен единице, если определитель второго порядка равен нулю, т.е.

§6. Системы линейных уравнений общего вида.

Система вида
---(9) называется системой общего вида.

Определение 31: Две системы называются равносильными (эквивалентными), если каждое решение первой системы являются решением второй и наоборот.

В системе (1) матрицу А=
назовем основной матрицей системы, а=
расширенной матрицей системы

Теорема. Кронекера-Капелли

Для совместности системы (9) необходим и достаточно, чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы, т. е. r(A)=r()

Теорема 1. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема 2. Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Правило решения произвольной системы линейных уравнений:

1)найти ранги основной и расширенной матриц системы. Если
, то система не совместна.

2) Если
=r, то система совместна. Найти какой-либо базисный минор порядкаr. Базисным будем называть минор, на основании которого определялся ранг матрицы.

Неизвестные, коэффициенты которых входят в базисный минор, называют главными (базисными) и оставляют слева, а остальные неизвестные называют свободными и переносят в правую часть уравнения.

3)Найти выражения главных неизвестных через свободные. Получено общее решение системы.

Пример 20: Исследовать систему и в случае ее совместности найти или единственное или общее решение

Решение: 1) по Т. Кронекера-Капелли находим ранги расширенной и основной матриц системы:

~
~

~
~
ранг основной матрицы равен двум

2) находим ранг расширенной матрицы
~
~
~

3) Вывод:
=2, то система совместна.

Но

система неопределенная и имеет бесчисленное множество решений.

4) Базисные неизвестные и, т. к. они принадлежат базисному минору, а- свободная неизвестная.

Пусть =с, где с – любое число.

5)Последней матрице соответствует система

6)Ответ:

7) Проверка: в любое из уравнений исходной системы, где присутствуют все неизвестные, подставляем найденные значения.

В каждой матрице можно связать два ранга: строчный ранг (ранг системы строк) и столбцовый ранг (ранг системы столбцов).

Теорема

Строчный ранг матрицы равен её столбцовому рангу.

Ранг матрицы

Определение

Рангом матрицы $A$ называется ранг её системы строк или столбцов.

Обозначается $\operatorname{rang} A$

На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.

Элементарные преобразования над строками (столбцами) матрицы не меняют её ранга.

Ранг ступенчатой матрицы равен количеству её ненулевых строк.

Пример

Задание. Найти ранг матрицы $ A=\left(\begin{array}{cccc}{0} & {4} & {10} & {1} \\ {4} & {8} & {18} & {7} \\ {10} & {18} & {40} & {17} \\ {1} & {7} & {17} & {3}\end{array}\right) $

Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:

$$ A \sim \left(\begin{array}{cccc}{0} & {4} & {10} & {1} \\ {4} & {8} & {18} & {7} \\ {2} & {2} & {4} & {3} \\ {1} & {7} & {17} & {3}\end{array}\right) $$

От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых:

$$ A \sim \left(\begin{array}{rrrr}{0} & {4} & {10} & {1} \\ {0} & {-20} & {-50} & {-5} \\ {0} & {-12} & {-30} & {-3} \\ {1} & {7} & {17} & {3}\end{array}\right) $$

Ко второй строке прибавим пять первых, к третьей - три третьих:

$$ A \sim \left(\begin{array}{cccc}{0} & {4} & {10} & {1} \\ {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0} \\ {1} & {7} & {17} & {3}\end{array}\right) $$

Меняем местами первую и вторую строчки:

$$ A \sim \left(\begin{array}{cccc}{0} & {0} & {0} & {0} \\ {0} & {4} & {10} & {1} \\ {0} & {0} & {0} & {0} \\ {1} & {7} & {17} & {3}\end{array}\right) $$

$$ A \sim \left(\begin{array}{cccc}{1} & {7} & {17} & {3} \\ {0} & {4} & {10} & {1} \\ {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0}\end{array}\right) \Rightarrow \operatorname{rang} A=2 $$

Ответ. $ \operatorname{rang} A=2 $

Метод окаймления миноров

На этой теореме базируется еще один метод нахождения ранга матрицы - метод окаймления миноров . Суть этого метода заключается в нахождении миноров, начиная с низших порядков и двигаясь к более высоким. Если минор $n$-го порядка не равен нулю, а все миноры $n+1$-го равны нулю, то ранг матрицы будет равен $n$ .

Пример

Задание. Найти ранг матрицы $ A=\left(\begin{array}{rrrr}{1} & {2} & {-1} & {-2} \\ {2} & {4} & {3} & {0} \\ {-1} & {-2} & {6} & {6}\end{array}\right) $ , используя метод окаймления миноров.

Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам матрицы $A$ . Рассмотрим, например, минор $ M_{1}=1 \neq 0 $ . расположенный в первой строке и первом столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор $ M_{2}^{1}=\left| \begin{array}{ll}{1} & {2} \\ {2} & {4}\end{array}\right|=0 $ ; рассмотрим еще один минор второго порядка, для этого минор $M_1$ окаймляем при помощи второй строки и третьего столбца, тогда имеем минор $ M_{2}^{2}=\left| \begin{array}{rr}{1} & {-1} \\ {2} & {3}\end{array}\right|=5 \neq 0 $ , то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор $ M_{2}^{2} $ . Таких миноров два: комбинация третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры.

Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r , то это означает, что в матрице А имеется отличный от нуля минор порядка r , но всякий минор порядка, большего чем r , равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение

Вычисление ранга матрицы с помощью миноров

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k .

Пример 1. Найти методом окаймления миноров ранг матрицы

.

Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М 1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M 2 = , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М 2 . Их всего два (можно добавить второй столбец или четвертый). Вычисляем их: = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

Вычисление ранга матрицы с помощью элементарных преобразований

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными , если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,

.

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Пример 2 Найти ранг матрицы

и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

.

Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

;

из третьей строки вычтем первую; получим матрицу

которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

.

Для работы с понятием ранга матрицы нам понадобятся сведения из темы "Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений" . В первую очередь это касается термина "минор матрицы" , так как ранг матрицы станем определять именно через миноры.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Эквивалентные матрицы - матрицы, ранги которых равны между собой.

Поясним подробнее. Допустим, среди миноров второго порядка есть хотя бы один, отличный от нуля. А все миноры, порядок которых выше двух, равны нулю. Вывод: ранг матрицы равен 2. Или, к примеру, среди миноров десятого порядка есть хоть один, не равный нулю. А все миноры, порядок которых выше 10, равны нулю. Вывод: ранг матрицы равен 10.

Обозначается ранг матрицы $A$ так: $\rang A$ или $r(A)$. Ранг нулевой матрицы $O$ полагают равным нулю, $\rang O=0$. Напомню, что для образования минора матрицы требуется вычёркивать строки и столбцы, - однако вычеркнуть строк и столбцов более, чем содержит сама матрица, невозможно. Например, если матрица $F$ имеет размер $5\times 4$ (т.е. содержит 5 строк и 4 столбца), то максимальный порядок её миноров равен четырём. Миноры пятого порядка образовать уже не удастся, так как для них потребуется 5 столбцов (а у нас всего 4). Это означает, что ранг матрицы $F$ не может быть больше четырёх, т.е. $\rang F≤4$.

В более общей форме вышеизложенное означает, что если матрица содержит $m$ строк и $n$ столбцов, то её ранг не может превышать наименьшего из чисел $m$ и $n$, т.е. $\rang A≤\min(m,n)$.

В принципе, из самого определения ранга следует метод его нахождения. Процесс нахождения ранга матрицы по определению можно схематически представить так:

Поясню эту схему более подробно. Начнём рассуждать с самого начала, т.е. с миноров первого порядка некоторой матрицы $A$.

1. Если все миноры первого порядка (т.е. элементы матрицы $A$) равны нулю, то $\rang A=0$. Если среди миноров первого порядка есть хотя бы один, не равный нулю, то $\rang A≥ 1$. Переходим к проверке миноров второго порядка.
2. Если все миноры второго порядка равны нулю, то $\rang A=1$. Если среди миноров второго порядка есть хотя бы один, не равный нулю, то $\rang A≥ 2$. Переходим к проверке миноров третьего порядка.
3. Если все миноры третьего порядка равны нулю, то $\rang A=2$. Если среди миноров третьего порядка есть хотя бы один, не равный нулю, то $\rang A≥ 3$. Переходим к проверке миноров четвёртого порядка.
4. Если все миноры четвёртого порядка равны нулю, то $\rang A=3$. Если среди миноров четвёртого порядка есть хотя бы один, не равный нулю, то $\rang A≥ 4$. Переходим к проверке миноров пятого порядка и так далее.

Что ждёт нас в конце этой процедуры? Возможно, что среди миноров k-го порядка найдётся хоть один, отличный от нуля, а все миноры (k+1)-го порядка будут равны нулю. Это значит, что k - максимальный порядок миноров, среди которых есть хотя бы один, не равный нулю, т.е. ранг будет равен k. Может быть иная ситуация: среди миноров k-го порядка будет хоть один не равный нулю, а миноры (k+1)-го порядка образовать уже не удастся. В этом случае ранг матрицы также равен k. Короче говоря, порядок последнего составленного ненулевого минора и будет равен рангу матрицы .

Перейдём к примерам, в которых процесс нахождения ранга матрицы по определению будет проиллюстрирован наглядно. Ещё раз подчеркну, что в примерах данной темы мы станем находить ранг матриц, используя лишь определение ранга. Иные методы (вычисление ранга матрицы методом окаймляющих миноров , вычисление ранга матрицы методом элементарных преобразований) рассмотрены в следующих темах.

Кстати, вовсе не обязательно начинать процедуру нахождения ранга с миноров самого малого порядка, как это сделано в примерах №1 и №2. Можно сразу перейти к минорам более высоких порядков (см. пример №3).

Пример №1

Найти ранг матрицы $A=\left(\begin{array}{ccccc} 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end{array} \right)$.

Данная матрица имеет размер $3\times 5$, т.е. содержит три строки и пять столбцов. Из чисел 3 и 5 минимальным является 3, посему ранг матрицы $A$ не больше 3, т.е. $\rang A≤ 3$. И это неравенство очевидно, так как миноры четвёртого порядка образовать мы уже не сможем, - для них нужно 4 строки, а у нас всего 3. Перейдём непосредственно к процессу нахождения ранга заданной матрицы.

Среди миноров первого порядка (т.е среди элементов матрицы $A$) есть ненулевые. Например, 5, -3, 2, 7. Вообще, нас не интересует общее количество ненулевых элементов. Есть хотя бы один не равный нулю элемент - и этого достаточно. Так как среди миноров первого порядка есть хотя бы один, отличный от нуля, то делаем вывод, что $\rang A≥ 1$ и переходим к проверке миноров второго порядка.

Начнём исследовать миноры второго порядка. Например, на пересечении строк №1, №2 и столбцов №1, №4 расположены элементы такого минора: $\left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|$. У этого определителя все элементы второго столбца равны нулю, поэтому и сам определитель равен нулю, т.е. $\left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|=0$ (см. свойство №3 в теме свойства определителей). Или же можно банально вычислить сей определитель, используя формулу №1 из раздела по вычислению определителей второго и третьего порядков :

$$ \left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|=5\cdot 0-0\cdot 7=0. $$

Первый проверенный нами минор второго порядка оказался равен нулю. О чём это говорит? О том, что нужно дальше проверять миноры второго порядка. Либо они все окажутся нулевыми (и тогда ранг будет равен 1), либо среди них найдётся хотя бы один минор, отличный от нуля. Попробуем осуществить более удачный выбор, записав минор второго порядка, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №5: $\left|\begin{array}{cc} 5 & 2 \\ 7 & 3 \end{array} \right|$. Найдём значение этого минора второго порядка:

$$ \left|\begin{array}{cc} 5 & 2 \\ 7 & 3 \end{array} \right|=5\cdot 3-2\cdot 7=1. $$

Данный минор не равен нулю. Вывод: среди миноров второго порядка есть хотя бы один, отличный от нуля. Следовательно $\rang A≥ 2$. Нужно переходить к исследованию миноров третьего порядка.

Если для формирования миноров третьего порядка мы станем выбирать столбец №2 или столбец №4, то такие миноры будут равными нулю (ибо они будут содержать нулевой столбец). Остаётся проверить лишь один минор третьего порядка, элементы которого расположены на пересечении столбцов №1, №3, №5 и строк №1, №2, №3. Запишем этот минор и найдём его значение:

$$ \left|\begin{array}{ccc} 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end{array} \right|=-20-18-14+16+21+15=0. $$

Итак, все миноры третьего порядка равны нулю. Последний составленный нами ненулевой минор был второго порядка. Вывод: максимальный порядок миноров, среди которых есть хотя бы один, отличный от нуля, равен 2. Следовательно, $\rang A=2$.

Ответ : $\rang A=2$.

Пример №2

Найти ранг матрицы $A=\left(\begin{array} {cccc} -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end{array} \right)$.

Имеем квадратную матрицу четвёртого порядка. Сразу отметим, что ранг данной матрицы не превышает 4, т.е. $\rang A≤ 4$. Приступим к нахождению ранга матрицы.

Среди миноров первого порядка (т.е среди элементов матрицы $A$) есть хотя бы один, не равный нулю, поэтому $\rang A≥ 1$. Переходим к проверке миноров второго порядка. Например, на пересечении строк №2, №3 и столбцов №1 и №2 получим такой минор второго порядка: $\left| \begin{array} {cc} 4 & -2 \\ -5 & 0 \end{array} \right|$. Вычислим его:

$$ \left| \begin{array} {cc} 4 & -2 \\ -5 & 0 \end{array} \right|=0-10=-10. $$

Среди миноров второго порядка есть хотя бы один, не равный нулю, поэтому $\rang A≥ 2$.

Перейдём к минорам третьего порядка. Найдём, к примеру, минор, элементы которого расположены на пересечении строк №1, №3, №4 и столбцов №1, №2, №4:

$$ \left | \begin{array} {cccc} -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end{array} \right|=105-105=0. $$

Так как данный минор третьего порядка оказался равным нулю, то нужно исследовать иной минор третьего порядка. Либо все они окажутся равными нулю (тогда ранг будет равен 2), либо среди них найдётся хоть один, не равный нулю (тогда станем исследовать миноры четвёртого порядка). Рассмотрим минор третьего порядка, элементы которого расположены на пересечении строк №2, №3, №4 и столбцов №2, №3, №4:

$$ \left| \begin{array} {ccc} -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end{array} \right|=-28. $$

Среди миноров третьего порядка есть хотя бы один, отличный от нуля, поэтому $\rang A≥ 3$. Переходим к проверке миноров четвёртого порядка.

Любой минор четвёртого порядка располагается на пересечении четырёх строк и четырёх столбцов матрицы $A$. Иными словами, минор четвёртого порядка - это определитель матрицы $A$, так как данная матрица как раз и содержит 4 строки и 4 столбца. Определитель этой матрицы был вычислен в примере №2 темы "Понижение порядка определителя. Разложение определителя по строке (столбцу)" , поэтому просто возьмём готовый результат:

$$ \left| \begin{array} {cccc} -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end{array} \right|=86. $$

Итак, минор четвертого порядка не равен нулю. Миноров пятого порядка образовать мы уже не можем. Вывод: наивысший порядок миноров, среди которых есть хотя бы один отличный от нуля, равен 4. Итог: $\rang A=4$.

Ответ : $\rang A=4$.

Пример №3

Найти ранг матрицы $A=\left(\begin{array} {cccc} -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end{array} \right)$.

Сразу отметим, что данная матрица содержит 3 строки и 4 столбца, поэтому $\rang A≤ 3$. В предыдущих примерах мы начинали процесс нахождения ранга с рассмотрения миноров наименьшего (первого) порядка. Здесь же попробуем сразу проверить миноры максимально возможного порядка. Для матрицы $A$ такими являются миноры третьего порядка. Рассмотрим минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №4:

$$ \left| \begin{array} {ccc} 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end{array} \right|=-8-60-20=-88. $$

Итак, наивысший порядок миноров, среди которых есть хоть один, не равный нулю, равен 3. Поэтому ранг матрицы равен 3, т.е. $\rang A=3$.

Ответ : $\rang A=3$.

Вообще, нахождение ранга матрицы по определению - в общем случае задача довольно-таки трудоёмкая. Например у матрицы сравнительно небольшого размера $5\times 4$ имеется 60 миноров второго порядка. И если даже 59 из них будут равны нулю, то 60й минор может оказаться ненулевым. Тогда придётся исследовать миноры третьего порядка, которых у данной матрицы 40 штук. Обычно стараются использовать менее громоздкие способы, такие как метод окаймляющих миноров или метод эквивалентных преобразований .